우선순위 큐(Priority queue)
1. 정의: 각 요소에 우선순위가 할당된 큐
2. 특징:
- 높은 우선순위 요소가 먼저 처리됨
- 동적으로 요소 추가/제거 가능
3. 주요 연산:
- 삽입: 새 요소 추가
- 최대값 추출: 최고 우선순위 요소 제거 및 반환
- 우선순위 변경: 요소의 우선순위 수정
우선순위 기반 데이터 관리에 효과적이고 주로 큐로 구현합니다.
우선순위 큐 특징
1. 동적 집합 S를 유지합니다. 이는 요소들이 추가되거나 제거될 수 있음을 의미합니다.
초기 상태:
S = { } (빈 집합)
요소 추가 후:
S = { 5, 3, 8 }
또 다른 요소 추가:
S = { 5, 3, 8, 1 }
요소 제거 후:
S = { 5, 8, 1 }
2. 각 집합의 요소는 키(key)라고 하는 연관된 값을 가집니다. 이 키는 요소의 우선순위를 결정합니다.
요소1: (데이터: "작업A", 키: 5)
요소2: (데이터: "작업B", 키: 3)
요소3: (데이터: "작업C", 키: 8)요소3이 가장 우선순위(8)가 높으니 먼저 처리됩니다.
3. 최대 우선순위 큐는 다음과 같은 동적 집합 연산을 지원합니다:
a. INSERT(S, x): 요소 x를 집합 S에 삽입합니다.
b. MAXIMUM(S): S에서 가장 큰 키를 가진 요소를 반환합니다.
c. EXTRACT-MAX(S): S에서 가장 큰 키를 가진 요소를 제거하고 반환합니다.
d. INCREASE-KEY(S, x, k): 요소 x의 키 값을 k로 증가시킵니다. 단, k는 x의 현재 키 값보다 크거나 같아야 합니다.
이러한 연산들을 통해 우선순위 큐는 항상 가장 높은 우선순위(여기서는 가장 큰 키 값)를 가진 요소에 빠르게 접근하고 조작할 수 있습니다. 이는 다양한 알고리즘과 응용 프로그램에서 유용하게 사용됩니다.
우선순위 큐는 주로 힙(Heap) 자료구조를 사용하여 구현되며, 이를 통해 효율적인 연산이 가능합니다.
힙에대해서 모르겠다면 아래 포스트를 참고해주시기 바랍니다.
https://kimyir.tistory.com/106
힙, 힙 정렬이란 Heap, Heap Sort
저번 시간에 알고리즘의 뜻을 말했는데요. 대충 문제 해결 방식입니다.그럼 자료구조는 뭘까요? 자료 구조는 이름 그대로 자료의 구조. 즉 자료를 담는 방법입니다.그 중 힙은 정렬, 우선순위 큐
kimyir.tistory.com
힙으로 구현
HEAP-EXTRACT-MAX(S)

이제 우선 순위 큐의 힙 의사 코드를 봅시다.
단계적 설명
아까 EXTRACT-MAX(S)뜻이 "S에서 가장 큰 키를 가진 요소를 제거하고 반환합니다." 라고 했는데
코드를 보면 heap-size[A] 배열이 비어있지 않다면 루트 노드에 있는 최대값 A[1]을 저장해줍니다.
그리고 A[1]을 A[heap-size]번째, 즉 마지막 노드로 이동한 뒤, 힙 크기를 감소합니다.
이렇게 가장 우선순위(최대값) 노드를 얻었으면 MAX-HEAPIFY 작업을 하여 다시 최대힙으로 정렬해줍니다.
특징:
- 최대값 추출 후 힙 구조 유지
- 시간 복잡도: O(log n) (MAX-HEAPIFY 때문)
활용:
- 우선순위 큐 구현
- 힙 정렬 알고리즘의 일부
def heap_extract_max(A):
if len(A) - 1 < 1: # heap-size[A] < 1
raise ValueError("힙 언더플로우")
max_val = A[1] # max ← A[1]
A[1] = A[len(A) - 1] # A[1] ← A[heap-size[A]]
A[len(A) - 1] = None # 마지막 요소를 None으로 설정
A.heap_size -= 1 # heap-size[A] ← heap-size[A] - 1
max_heapify(A, 1) # MAX-HEAPIFY(A, 1)
return max_val
# 사용 예
heap = [16, 14, 10, 8, 7, 9, 3, 2, 4, 1]
print("원래 힙:", heap)
max_val = heap_extract_max(heap)실제 예시 파이썬 코드입니다.
HEAP-INCREASE-KEY(A,i,key)
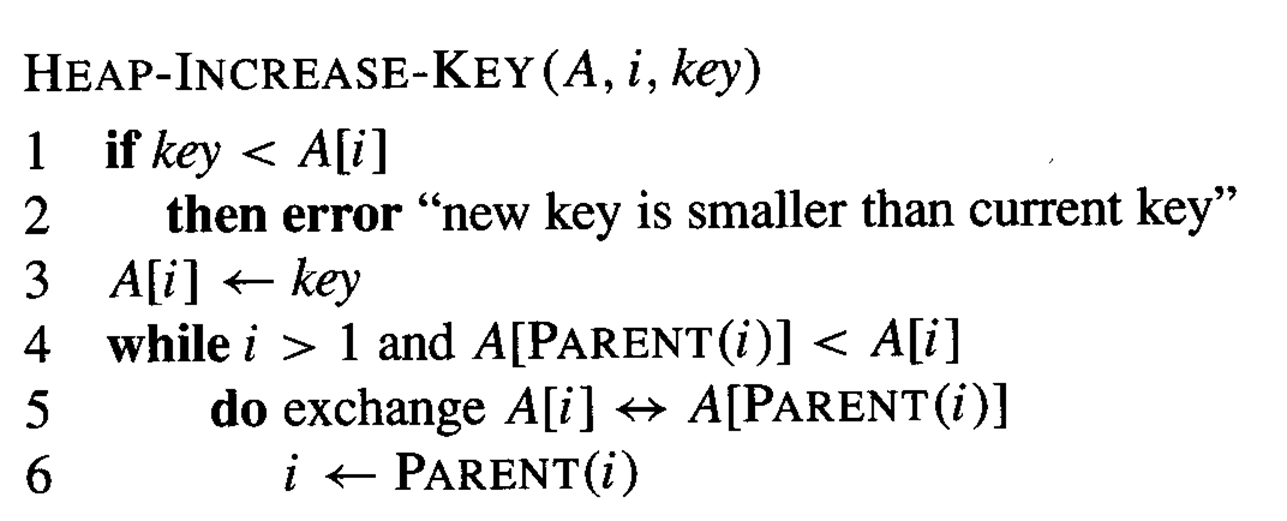
그 다음은 위에서 얘기한 INCREASE-KEY(S, x, k)의 의사코드입니다.
이 함수는 요소 x의 키 값을 k로 증가시킵니다.
단, k는 x의 현재 키 값보다 크거나 같아야 합니다. 최대 힙 속성을 유지 해야하기 때문입니다.
매개변수:
- A: 힙 배열
- i: 키를 증가시킬 노드의 인덱스
- key: 새로운 키 값
단계별 설명:
1) 새 키가 현재 키보다 작은지 확인
2) 노드의 키 값을 새 값으로 업데이트
3) 부모 노드와 비교하며 필요시 교환 (상향 이동)
값이 바뀌기 때문에 우선순위 큐에서 요소의 우선순위 변경할 수 있습니다.
또한 다익스트라 알고리즘 등에서 사용되는걸로 압니다.
MAX-HEAP-INSERT(A, key)
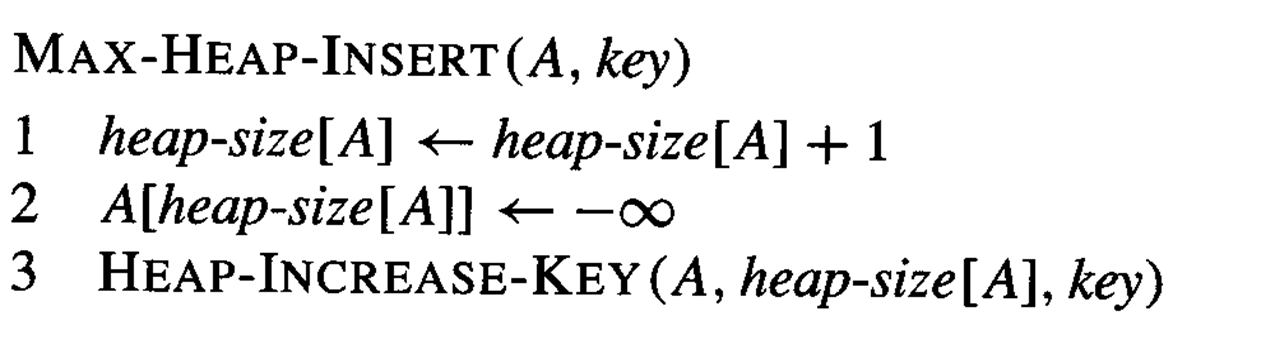
MAX-HEAP-INSERT(A, key), 위에서도 있었는데
INSERT(S, x) : 요소 x를 집합 S에 삽입합니다.
그럼 각각 S와 x를 A와 key로 대입하면
- A: 힙 배열
- key: 삽입할 새로운 키 값
가 되겠습니다.
단계별 설명:
1) 힙 크기를 1 증가시킵니다.
2) 새 노드를 힙의 마지막에 -∞ 값으로 추가합니다.
3) HEAP-INCREASE-KEY 함수를 호출하여 새 노드의 키 값을 설정하고 적절한 위치로 이동시킵니다.
주요 특징:
- 새 요소를 힙의 마지막에 추가한 후 상향식으로 조정
- 시간 복잡도: O(log n) (HEAP-INCREASE-KEY의 복잡도와 동일)
활용:
- 우선순위 큐에 새로운 요소 추가
- 힙 정렬 알고리즘의 일부로 사용
'그냥 개발글 > 알고리즘' 카테고리의 다른 글
| 정렬의 하한 - 3개 요소에 대한 삽입 정렬을 위한 결정 트리 (1) | 2024.10.20 |
|---|---|
| 퀵 정렬 Quick Sort (1) | 2024.10.19 |
| 힙, 힙 정렬이란 Heap, Heap Sort (0) | 2024.10.19 |
| 숫자 정렬 알고리즘 Sorting of Numbers (0) | 2024.10.19 |