
퀵 정렬의 하이라이트
이름 그대로 빠른 정렬이 가능한 알고리즘입니다.
핵심은 피벗(Pivot)입니다.
피벗은 또 다르게 파티션이라고도 부를 수 있습니다.
퀵 정렬은 불안정한 정렬인데 왜그런지는 뒤에서 설명하겠습니다.
어쨋든 퀵 정렬의 실행 시간은 다음과 같습니다.
최악의 경우 실행 시간: Θ(n^2).
기대 실행 시간: Θ(n lg n)
Θ(n lg n)에 숨겨진 상수는 작습니다.
제자리에서 정렬됩니다.
! 글에서 파티션은 피벗이라 생각해주시기 바랍니다. !
진짜 좋은 영상 있으니 참고
https://www.youtube.com/watch?v=Hoixgm4-P4M
퀵 정렬의 세가지 전략
나누기:
배열 A[p . . r ]에서 A[q]를 파티션(피벗)으로 삼아
두 개의 (아마도 비어 있는) 하위 배열 A[p . . q − 1] 및 A[q + 1 . . r ]로 분할합니다.
첫 번째 하위 배열 A[p 의 각 요소. . q − 1] 은 ≤ A[q] 이고 A[q] 는 ≤ 두 번째 하위 배열 A[q + 1 의 각 요소입니다. . r ]
이게 말이 어려운데 눈으로 이해해봅시다.

이렇게 A[p .. r] 과 피벗 A[q]를 잘 설정했습니다.
여기서 p는 배열의 시작 인덱스, r은 끝 인덱스입니다.
이렇게 선택한 피벗을 기준으로 왼쪽 오른쪽 정렬해봅시다.

이렇게 되면 배열이 두 부분으로 나뉩니다:
1. A[p..q-1]: [2, 1] (3보다 작은 요소들)
2. A[q+1..r]: [5, 7, 6, 9] (3보다 큰 요소들)
피벗 3은 자신의 올바른 위치에 있게 됩니다.
올바른 위치란 어려운게 아니라 이런식으로 피벗을 기준으로 작고 큰 요소들이 잘 배치되있으면 됩니다.
이렇게 분할된 두 부분 배열에 대해 재귀적으로 같은 과정을 반복하여 전체 배열을 정렬합니다.
정복:
QUICKSORT에 대한 재귀 호출을 통해 두 개의 하위 배열을 정렬합니다.
결합:
하위 배열은 제자리에 정렬되어 있으므로 결합하는 데 작업이 필요하지 않습니다.
파티션(피벗) 의사 코드

1. 피벗(x)으로 배열의 마지막 요소 선택
2. i는 작은 요소들의 경계를 추적
3. j로 배열을 순회하며:
- A[j]가 피벗보다 작거나 같으면 i를 증가시키고 A[i]와 A[j]를 교환
4. 마지막으로 피벗을 올바른 위치로 이동
5. 피벗의 최종 위치 반환
이 과정을 통해 배열이 피벗을 기준으로 두 부분으로 나뉘게 됩니다.
왼쪽은 피벗보다 작거나 같은 요소들, 오른쪽은 큰 요소들로 구성됩니다.

그리고 이 피벗 코드를 활용한 퀵 정렬 코드입니다.
1. 기본 조건: p < r 일 때만 정렬 수행 (배열 길이가 2 이상일 때)
2. PARTITION (피벗) 함수 호출:
- 배열을 두 부분으로 나누고 피벗의 위치 q를 반환
3. 재귀 호출:
- 피벗 왼쪽 부분 정렬: QUICKSORT(A, p, q-1)
- 피벗 오른쪽 부분 정렬: QUICKSORT(A, q+1, r)
이 알고리즘은 위에서 설명 드렸던 분할 정복 방식으로 작동합니다:
- 분할: PARTITION 함수로 배열을 나눔
- 정복: 나눠진 부분 배열을 재귀적으로 정렬
- 결합: 이미 정렬된 부분 배열들이 전체 정렬된 배열을 형성
이 과정을 반복하여 전체 배열이 정렬됩니다.
Worst Case
퀵소트의 최악의 경우(Worst-Case)
1. 불균형한 분할:
- 퀵정렬이 가장 비효율적으로 작동하는 경우입니다.
- 매 분할마다 한쪽 부분배열에 모든 요소가 몰리고, 다른 쪽은 비어있게 됩니다.
2. 구체적인 상황:
- 한 부분배열에는 0개의 요소
- 다른 부분배열에는 n-1개의 요소 (n은 전체 배열 크기)
3. 시간 복잡도 분석:
* T(n) = T(n-1) + T(0) + Θ(n)
각 부분을 보자면
* T(n-1): 큰 부분배열 처리 시간
최악의 경우, n-1개 요소가 한쪽 부분배열로 가게 됩니다. 그렇기 때문에 큰 부분배열인겁니다.
* T(0): 빈 부분배열 처리 시간 (무시 가능)
* Θ(n): 분할 과정의 시간
n개 요소를 모두 한 번씩 비교해야 하므로 Θ(n) 시간이 듭니다.
- 결국 무시하는걸 제외하면 아래 재귀식이 나옵니다.
T(n) = T(n-1) + Θ(n)
이걸 수학적으로 풀어봅시다
다시 말씀드리지만 지금 우리의 T(n)은 재귀식입니다.
배열을 계속 피벗을 정해서 정렬하고 쪼개기 때문에 재귀식입니다.
이 식은 모든 n에 대해 성립합니다. 따라서 n 대신 (n-1)을 넣어도 똑같이 성립합니다:
T(n-1) = T((n-1)-1) + Θ(n-1) = T(n-2) + Θ(n-1)
도 가능하다는거죠
이는 마치 수학에서 x = 2x - 3 이라는 식이 있을 때, x 대신 (x-1)을 넣어
(x-1) = 2(x-1) - 3 이라고 쓸 수 있는 것과 같은 원리입니다.
T(n) = T(n-1) + Θ(n)
= (T(n-2) + Θ(n-1)) + Θ(n)
= ((T(n-3) + Θ(n-2)) + Θ(n-1)) + Θ(n)
...
= T(1) + Θ(2) + Θ(3) + ... + Θ(n-1) + Θ(n)
이런식으로 유도를 하다보면 어느순간 T(n-1)은 이미 다 풀어진걸 볼 수 있습니다.
이제 정리하면
Θ(1 + 2 + 3 + ... + n) = Θ(n(n+1)/2) = Θ(n²)
즉 재귀식을 풀면 T(n) = Θ(n²)가 됩니다.
이런 최악의 상황은 이미 정렬된 배열이나 역순으로 정렬된 배열에서 발생할 수 있습니다.
Best Case
최선의 상황에선 다음과 같습니다.
1. 균형 잡힌 분할:
- 매 분할마다 배열이 거의 정확히 반으로 나뉩니다.
- 이는 퀵소트가 가장 효율적으로 작동하는 경우입니다.
2. 부분배열의 크기:
- 각 부분배열은 n/2 이하의 요소를 가집니다.
- 이는 완벽한 균형을 의미합니다.
3. 시간 복잡도 분석:
- T(n) = 2T(n/2) + Θ(n)
각 부분을 보자면
* 2T(n/2): 두 개의 n/2 크기 부분배열을 정렬하는 시간
* Θ(n): 분할 과정의 시간
- 이 재귀식을 풀면 T(n) = Θ(n lg n)이 됩니다.
(여기서 lg n은 log₂ n을 의미합니다)
결론적으로, 최선의 경우 퀵정렬의 시간 복잡도는 O(n log n)입니다.
이는 배열이 매번 거의 균등하게 분할될 때 달성됩니다. 이 경우, 대부분의 정렬 알고리즘 중에서 가장 빠른 성능을 보입니다.
평균 실행 시간
퀵 정렬의 평균 실행 시간은 최악의 경우보다 최상의 경우에 훨씬 더 가깝습니다.
한마디로 대부분의 경우에선 괜찮은 알고리즘이라는겁니다.
PARTITION이 항상 9:1 분할을 생성한다고 가정해봅시다.
이때의 재귀 식을 구합니다.
T(n) ≤ T(9n/10) + T(n/10) + Θ(n)
- T(9n/10): 큰 부분배열(90%)을 정렬하는 시간
- T(n/10): 작은 부분배열(10%)을 정렬하는 시간
- Θ(n): 분할 과정의 시간
셋 다 합하면 O(n lg n)이 걸립니다. 이는 최선의 경우와 같은 시간 복잡도입니다.
결론적으로, 퀵정렬은 완벽하게 균형 잡히지 않은 분할에서도 여전히 효율적으로 작동합니다.
9:1 정도의 불균형한 분할에서도 O(n lg n)의 시간 복잡도를 유지하며, 이는 퀵정렬이 실제 상황에서 왜 효과적인지를 보여줍니다.
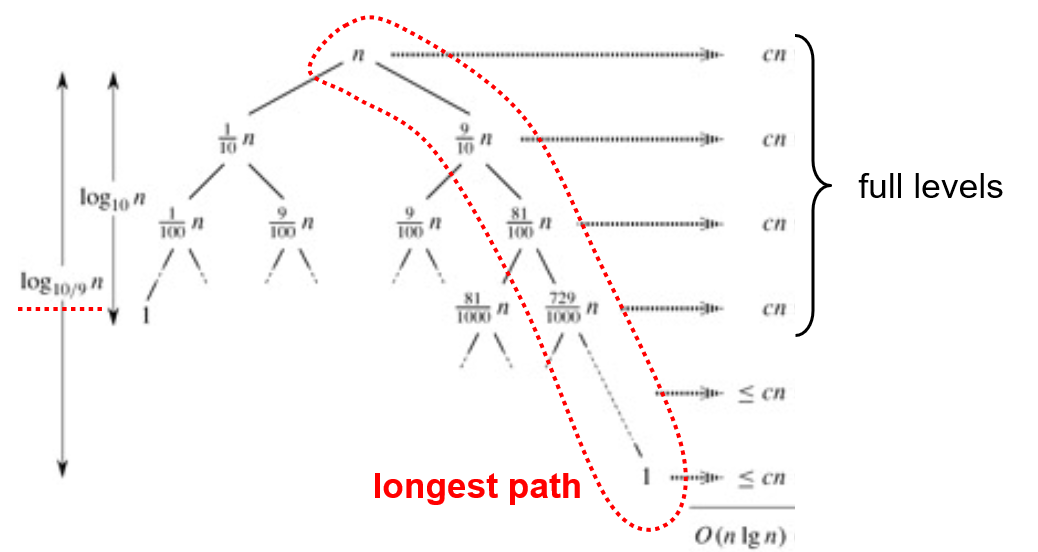
사진으로 보면 이렇습니다.
불안정한 퀵 정렬
재귀 트리의 분할은 항상 일정하지 않습니다.
일반적으로 재귀 트리 전체에는 좋은 분할과 나쁜 분할이 혼합되어 있습니다.
그렇기 때문에 불안정한 정렬이라는것입니다.
이것이 퀵 정렬의 점근적 실행 시간에 영향을 미치지 않는다는 것을 확인하기 위해
수준이 최상의 경우와 최악의 경우 분할 간에 번갈아 나타난다고 가정합니다.
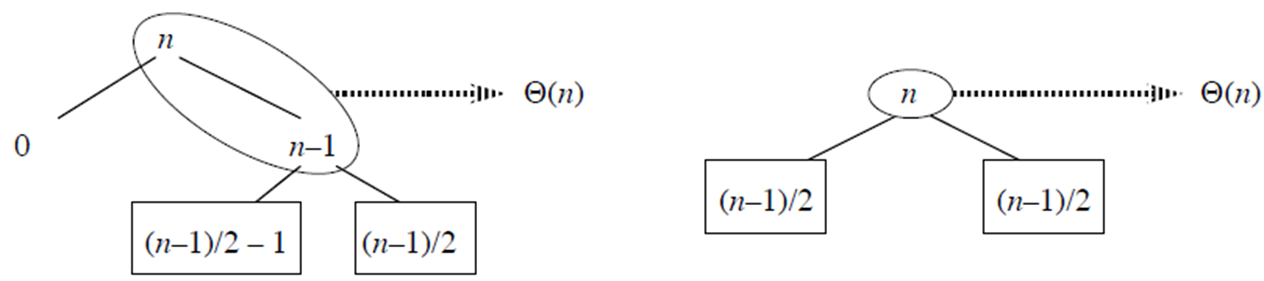
1. 두 그림 비교:
- 왼쪽 그림: 불균형한 분할을 보여줍니다 (0과 n-1로 나뉨).
- 오른쪽 그림: 균형 잡힌 분할을 보여줍니다 ((n-1)/2로 균등하게 나뉨).
2. 추가 레벨의 의미:
- 왼쪽 그림의 추가 레벨(0에서 n-1로 가는 단계)은 단순히 상수 시간을 추가합니다.
- 이는 빅오 표기법에서 숨겨진 상수에 영향을 줄 뿐, 전체적인 시간 복잡도에는 영향을 미치지 않습니다.
3. 부분배열의 수:
- 두 경우 모두 최종적으로 정렬해야 할 부분배열의 수는 동일합니다.
- 왼쪽 그림에서 추가 단계가 있지만, 결국 같은 크기의 부분배열로 나뉩니다.
4. 작업량:
- 왼쪽 그림의 경우, 추가 단계로 인해 최종 분할에 도달하기까지 약 두 배의 작업이 필요합니다.
- 하지만 이는 시간 복잡도의 차수(order)를 변경하지 않습니다.
결론적으로, 이 분석은 퀵소트의 평균적인 성능이 최악의 경우보다 최선의 경우에 더 가깝다는 것을 보여줍니다. 불균형한 분할이 발생하더라도, 전체적인 시간 복잡도는 여전히 O(n log n)에 가깝게 유지됩니다.
랜덤 퀵 정렬의 경우
그럼 항상 퀵 정렬은 최상의 경우일까요? 당연히 아닙니다.
이걸 보여주기 위해 랜덤 퀵 정렬을 예시를 들어봅시다.

시작에서도 말했지만 알고리즘의 주요 비용은 파티셔닝(피벗 정하기)입니다.
PARTITION은 매번 향후 고려 사항에서 피벗 요소를 제거합니다.
따라서 PARTITION은 최대 n번 호출됩니다.
PARTITION에 대한 각 호출이 수행하는 작업량은 상수에 해당 for 루프에서 수행되는 비교 횟수를 더한 것입니다.
X = PARTITION에 대한 모든 호출에서 수행된 총 비교 수라고 합니다.
따라서 전체 실행에 걸쳐 수행된 총 작업은 O(n + X)입니다.
분석을 쉽게 하기 위해:
A의 요소 이름을 z1, z2, 로 바꿉니다. . . , zn, zi는 i번째로 작은 요소입니다.

위 집합은 Zi와 Zj 사이의 요소 집합입니다.

중요한 부분은 각 요소 쌍은 최대 한 번만 비교됩니다.
요소는 피벗 요소하고만 비교되고 피벗 요소는 나중에 PARTITION을 호출할 때 절대 사용되지 않기 때문입니다.
각 쌍은 최대 한 번 비교되므로 알고리즘에 의해 수행되는 총 비교 횟수는 다음과 같습니다.
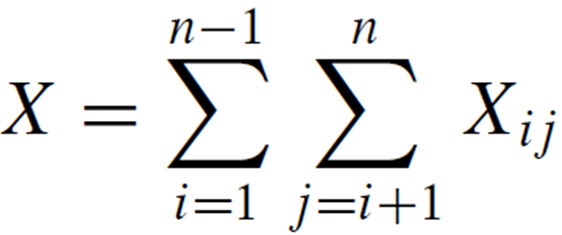
각 왼쪽 오른쪽 배열 양측의 기대값은 다음과 같습니다.
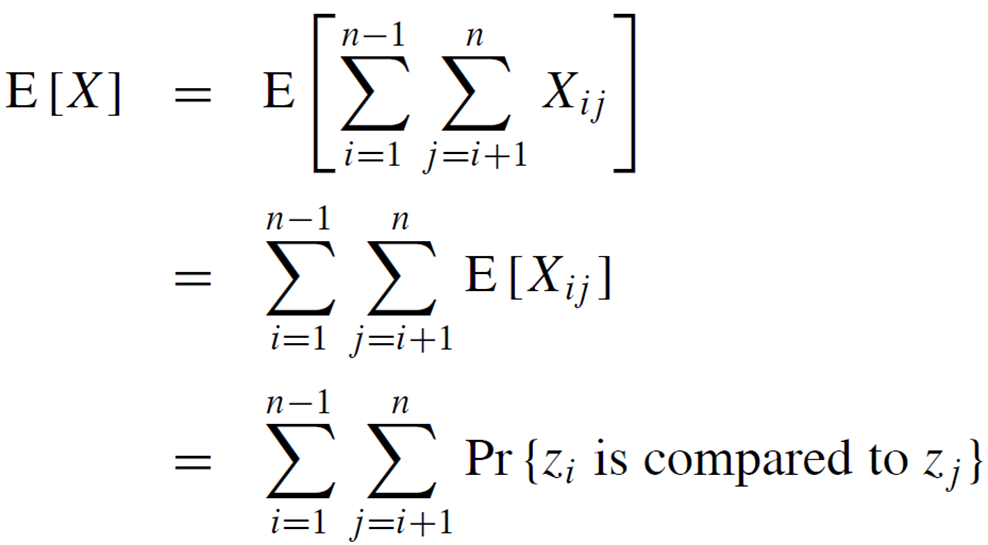
[3, 7, 1, 9, 5] 라는 배열이 있다고 가정합시다.
이 중 하나를 피벗으로 선택합니다. 예를 들어 5를 선택했다고 합시다.
5를 기준으로 배열을 나누면: [3, 1] 5 [7, 9]
이제 3과 7은 절대 서로 비교되지 않을 것입니다.
왜냐하면 3은 항상 5의 왼쪽에, 7은 항상 5의 오른쪽에 있을 것이기 때문입니다.
반면, 3과 1은 서로 비교될 가능성이 있습니다.
왜냐하면 둘 다 5보다 작은 부분에 속해 있기 때문입니다.
따라서, 두 요소가 비교될 확률은 그 두 요소 사이의 값이 피벗으로 선택되지 않을 확률과 관련이 있습니다.
또한, 둘 중 하나가 먼저 피벗으로 선택될 경우, 그 요소는 다른 모든 요소와 비교됩니다.
이런 방식으로 퀵 정렬의 평균적인 비교 횟수를 계산할 수 있습니다.
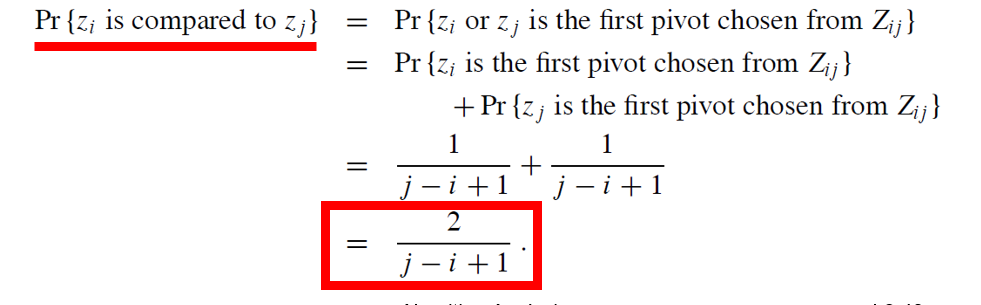
1. j - i + 1개의 요소가 있고, 피벗은 무작위로 독립적으로 선택됩니다.
i는 부분 배열의 시작 인덱스
j는 부분 배열의 끝 인덱스라고 보시면 됩니다.
2. 특정 요소가 첫 번째로 선택될 확률은 1/(j-i+1)입니다.
3. Zi와 Zj가 비교될 확률은 둘 중 하나가 첫 번째 피벗으로 선택될 확률과 같습니다.
4. 이 확률은 다음과 같이 계산됩니다:
Zi가 첫 피벗으로 선택될 확률 (1/(j-i+1))
Zj가 첫 피벗으로 선택될 확률 (1/(j-i+1))
따라서 총 확률은 2/(j-i+1)이 됩니다.
결과적으로 이 분석을 통해 퀵 정렬의 평균 시간 복잡도가 O(n log n)임을 증명할 수 있습니다.
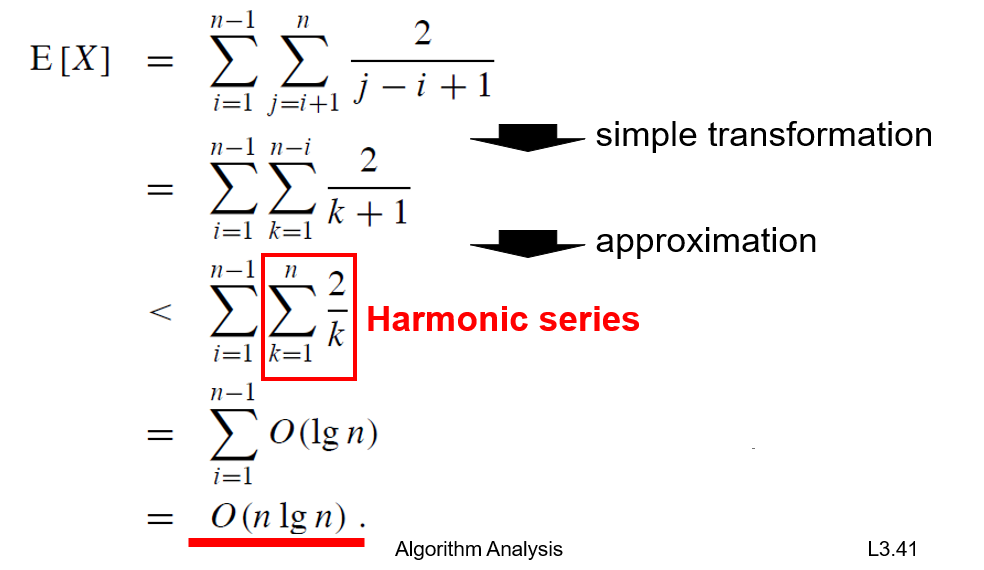
퀵 정렬의 평균 케이스에서 비교 횟수의 기댓값 E[X]를 계산하는 과정을 보여줍니다. 단계별로 설명하겠습니다:
1. 첫 번째 식:
- 모든 가능한 (i, j) 쌍에 대해 비교 확률(2/(j-i+1))의 합을 구합니다.
2. 변환 (simple transformation):
- j-i를 k로 치환하여 식을 단순화합니다.
3. 근사 (approximation):
- k+1을 k로 근사하여 계산을 단순화합니다.
4. 조화수열 (Harmonic series):
- 내부 합이 조화수열의 형태가 됩니다. (1/1 + 1/2 + 1/3 + ... + 1/n)
5. 최종 결과:
- 조화수열의 합은 대략 O(lg n)입니다.
- 외부 합으로 인해 n이 곱해져 최종적으로 O(n lg n)이 됩니다.
이 분석을 통해 퀵 정렬의 평균 시간 복잡도가 O(n lg n)임을 수학적으로 증명합니다.
'그냥 개발글 > 알고리즘' 카테고리의 다른 글
| Counting Sort 계수 정렬 (0) | 2024.10.20 |
|---|---|
| 정렬의 하한 - 3개 요소에 대한 삽입 정렬을 위한 결정 트리 (1) | 2024.10.20 |
| 우선순위 큐 Priority Queues (0) | 2024.10.19 |
| 힙, 힙 정렬이란 Heap, Heap Sort (0) | 2024.10.19 |