
그래프 순회는 그래프 내의 정점을 한번씩 살펴보기 위해 방문하는 것입니다.
이 순회에는 두 가지 BFS와 DFS 방식이 있습니다.
BFS는 친구에게 소문 퍼지듯이 가까운 사람부터 탐색하는것이고,
DFS는 미로에서 출구 찾듯이 한 길로 처음부터 끝까지 하는 것입니다.
더 자세하게 다루기 위해 포스팅 시작하겠습니다.
BFS
BFS(Breadth-First Search)란 시작 정점을 기준으로 인접한 가까운 정점들을 먼저 방문하는 방식입니다.
입력 :
방향, 또는 무방향 Graph G = (V, E)
source vertex는 시작 정점입니다.
s ∈ V (시작 정점 s는 정점 집합 V에 포함된다) 간단히 말해서 그냥 그래프의 정점에 포함되야 시작 정점일 수 있다는겁니다.
출력 :
d[v] : 시작점 s에서 정점 v까지의 거리,
이 거리는 무조건 최소 거리여야합니다. 즉 가장 적은 수의 간선이 쓰이는 길인거죠
이때 v ∈ V (v는 그래프에 포함되는 정점이어야한다는 말)
π[v] : 시작점 s에서 v까지의 최단 경로에서 마지막 간선 (u, v)의 u값
만약 경로가 1->3->5라면 마지막 간선인 (3, 5)에서 3을 저장한게 π[5] 입니다.
u는 v의 이전 정점이기 때문에 u is v's predecessor(선행자) 라는 말 기억해두시면 좋습니다.
BFS의 아이디어
시작 때 BFS는 소문 퍼지는거랑 비슷하다고 했는데요, 또 다른 예시로는 파도타기가 있습니다.
시작 정점인 s에서부터 파도를 보냅니다.
→ 먼저 s에서 1개의 간선으로 갈 수 있는 모든 정점을 방문합니다.
→ 그 다음 s에서 2개의 간선으로 갈 수 있는 모든 정점을 방문합니다.
→ 이런 식으로 계속 진행합니다.
특징
파도의 최전선을 유지하기 위해 FIFO 큐를 사용합니다. 처음 것이 들어오고 나가는 것이죠.
정점 v가 큐 Q에 있다는 것은 파도가 v에 도달했지만 아직 v에서 다른 정점으로 퍼져나가지 않았다는 의미입니다.
v ∈ Q 이렇게 표현 가능합니다.
BFS의 의사 코드

1. 시작점에서 가까운 정점부터 차례로 방문
2. 각 정점까지의 최단 거리를 계산
3. 최단 경로를 추적할 수 있는 정보(π)를 저장
더 보기 편하게 주석 달아드리겠습니다.
# 시작점 s를 제외한 모든 정점에 대해
for u in (모든 정점 - {s}):
color[u] = WHITE # 미방문 상태
d[u] = 무한대 # 거리를 무한대로 초기화
π[u] = NIL # 이전 정점 없음
# 시작점 s 초기화
color[s] = GRAY # 방문 중 상태
d[s] = 0 # 시작점까지 거리는 0
π[s] = NIL # 시작점의 이전 정점 없음
Q = [] # 빈 큐 생성
Q.append(s) # 시작점을 큐에 넣음
# 큐가 빌 때까지 반복
while Q:
u = Q.popleft() # 큐에서 정점 하나 꺼냄
# u와 연결된 모든 정점 v에 대해
for v in Adj[u]:
# v를 아직 방문하지 않았다면
if color[v] == WHITE:
color[v] = GRAY # 방문 중 표시
d[v] = d[u] + 1 # 거리 계산
π[v] = u # 이전 정점 저장
Q.append(v) # v를 큐에 넣음
color[u] = BLACK # u 방문 완료
각 색에 따라 상태가 다릅니다.
WHITE (흰색)
- 아직 방문하지 않은 정점
- 초기 상태의 모든 정점
GRAY (회색)
- 현재 방문 중인 정점
- 큐에 들어있는 상태
- "frontier" 또는 "경계" 정점
BLACK (검은색)
- 방문이 완전히 끝난 정점
- 이웃을 모두 확인한 정점
BFS 예시
아래 사진이 BFS로 거리 연산된 그래프입니다.
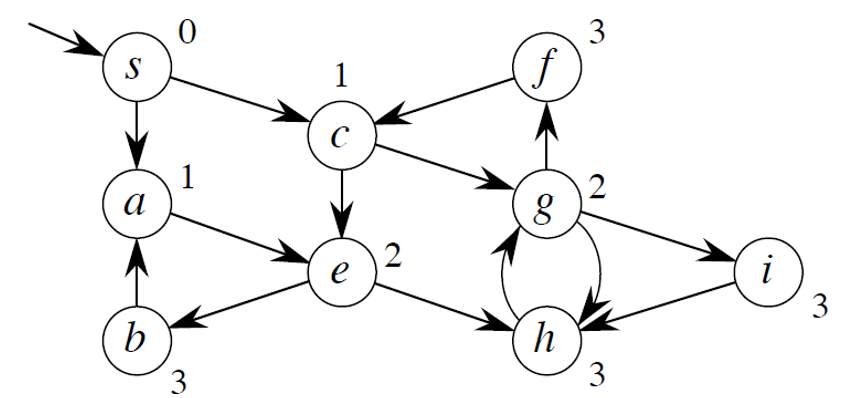
1. s에서 시작 (거리 0)
2. s의 이웃들(a, c) 방문 (거리 1)
3. a와 c의 이웃들(e, g) 방문 (거리 2)
4. e와 g의 이웃들(b, f, h, i) 방문 (거리 3)
각 숫자는 시작점 s에서 해당 정점까지 가는데 필요한 최소 간선 수를 나타냅니다.
BFS 특성
큐에는 거리 값 i 또는 i+1을 가진 정점들만 존재
예: 거리가 2인 정점들과 3인 정점들만 큐에 있을 수 있음
- 절대로 거리 차이가 2 이상 나는 정점들이 동시에 큐에 있을 수 없음
- 항상 작은 거리 값을 가진 정점들이 먼저 처리됨
거리 값은 무조건 단조 증가(계속 증가만 함, 감소 x), monotonically increasing
- 각 정점은 한 번만 방문됨
- 한번 할당된 거리 값은 변하지 않음
- 시간이 지날수록 더 먼 거리의 정점들이 방문됨
도달 불가능성
- BFS가 모든 정점을 방문하지 못할 수 있음
- 시작점에서 도달할 수 없는 정점이 있을 수 있음
예: 방향 그래프에서 시작점에서 가는 경로가 없는 정점
BFS 시간 복잡도
Time = O(V+E)
- V는 정점(Vertex)의 수
- 각 정점은 최대 한 번만 큐에 들어감
- 한번 방문한 정점은 다시 방문하지 않음
- E는 간선(Edge)의 수
- 각 간선은 정점이 큐에서 나올 때 한 번씩만 검사됨
- 방향 그래프: 각 간선은 정확히 한 번 검사
- 무방향 그래프: 각 간선은 최대 두 번 검사 (양쪽 정점에서 각각)
DFS
DFS(Depth-First Search)란 탐색중인 노드를 을 기준으로 한 방향으로 최대한 깊이 방문하는 방식입니다.
입력 :
방향, 또는 무방향 Graph G = (V, E)
source vertex는 없습니다!
출력 :
아까 BFS와 다르게 여기선 거리가 아닌 시간이 기준입니다.
각 정점에 대해 2개의 타임스탬프(timestamps)가 기록됩니다.
d[v] : 해당 정점을 처음 발견한 시간 (discovery time)
f[v] : 해당 정점의 탐색을 완료한 시간 (finishing time)
DFS의 아이디어
DFS는 깊이 우선으로 탐색하는데, 예시로는 미로탐험이 있습니다.
시작 정점은 없으므로 임의의 노드에서부터 미로를 탐험합니다.
→ 먼저 임의의 노드에서 갈 수 있는 길 중 하나를 선택해 끝까지 탐험합니다.
→ 더 이상 갈 수 없다면, 마지막 갈림길로 돌아와 새로운 길을 탐험합니다.
→ 모든 길을 탐험할 때까지 이 과정을 반복합니다.
특징
모든 간선을 체계적으로 탐색합니다.
필요한 경우 다른 정점에서 새로 시작 가능합니다.
정점을 발견하자마자 그 정점에서부터 탐색 시작합니다.
DFS는 이후 다른 알고리즘에서 유용하게 사용될 수 있습니다.
특히 타임스탬프 정보는 위상 정렬(Topological Sort)이나 강한 연결 요소 찾기(Strongly Connected Component) 등에 활용됩니다.
DFS 의사코드
# DFS 메인 함수: 그래프의 모든 정점을 탐색
DFS(V, E)
# 1단계: 모든 정점을 미방문(WHITE) 상태로 초기화
for each u ∈ V
do color[u] ← WHITE
time ← 0
# 2단계: 미방문 정점을 발견하면 DFS 탐색 시작
for each u ∈ V
do if color[u] = WHITE
then DFS-VISIT(u) # 해당 정점에서 DFS 탐색 시작
# DFS 방문 함수: 한 정점에서 시작하여 깊이 우선 탐색
DFS-VISIT(u)
color[u] ← GRAY # 현재 정점을 방문 중(GRAY) 상태로 변경
time ← time + 1
d[u] ← time # 현재 정점의 발견 시간 기록
# 현재 정점의 인접 정점들을 탐색
for each v ∈ Adj[u] # u의 모든 인접 정점 v에 대해
do if color[v] = WHITE # 미방문 상태라면
then DFS-VISIT(v) # 해당 정점으로 이동하여 탐색
color[u] ← BLACK # 현재 정점의 탐색을 완료(BLACK)
time ← time + 1
f[u] ← time # 현재 정점의 완료 시간 기록
각 색에 따라 상태가 다릅니다.
WHITE (흰색)
- 아직 방문하지 않은 정점
- 초기 상태의 모든 정점
GRAY (회색)
- 현재 방문 중인 정점
BLACK (검은색)
- 방문이 완전히 끝난 정점
타임스탬프 시간 기록시 규칙이 있습니다.
|V|는 전체 정점의 개수입니다.
각 정점은 두 개의 시간을 기록합니다:
d[v] = 발견 시간 (처음 방문했을 때)
f[v] = 완료 시간 (탐색을 끝냈을 때)
1부터 2|V|까지의 숫자 중 하나가 됨
항상 발견 시간 < 완료 시간
DFS 예시
아래 사진이 DFS로 연산된 그래프입니다.

뭔가 이상한 숫자가 둘로 쪼개져 있죠?
이를 이해할려면 Pre & Post 개념이 필요합니다.
https://youtu.be/2UvzjtJb-WQ?si=gaj_OzKTI0oQg-Ku
의문의 인도 형님 영상이 교수님보다 설명을 잘하시더군요
해당 동영상을 참고해서 작성했습니다.
Pre & Post의 다른 표현
Pre & Post = Start time & End time = Arrival & Departure
다 같은 표현입니다.
잘 보시면 time time 거리는데 아까 타임스탬프를 다뤘듯이 우린 시간을 기록해야합니다.
그래서 새로운 정점을 방문할 때마다 +1 (discovery time d[v])
정점 탐색 완료할 때마다 +1 (fininsh time f[v])
DFS에는 source vertex라는건 없지만, 임의로 지정한 최초 시작 정점에서 가장 먼저 이어져 있는(간선으로 연결된) 정점을
하나 찾고 해당 정점에 또 인접한 정점을 찾아 더 이상 깊이 갈 수 없을 때까지 탐색한 뒤 돌아오는 방식입니다.
이 때 탐색을 끝낸 뒤에 돌아오는 과정을 백트래킹이라고 합니다.
그래서 숫자 두개로 쪼개져 있는걸 다시 보시면 이건 탐색한 (시작 시간 | 종료 시간) 인겁니다.

그럼 과정을 한번 훑어볼까요?
일단 1에서 갈 수 있는 화살표 이웃은 2 5 8입니다. 가장 만만한 2부터 골라보죠 순서는 상관 없어요.
1 -> 2 -> 3 갔다가 끝내고 흠 하고 갈 곳 없으니 오케이 여기가 끝 하고 백트래킹합니다. 완료했으니까 4라고 기록합니다.
1로 백트래킹한 뒤 방문 안한 5로 갑시다.
흠 근데 또 5에서 갈곳이 없으니까 탐색 완료했다 치고 6으로 기록합니다.
5에서 백트래킹해서 3 -> 1 갔다가 탐색 완료 안한 2로 갑니다.
2 갔더니 갈곳이 없으니까 끝냈다 치고 7로 기록합니다.
이번엔 이웃 8에서 다시 출발합니다. 8-> 9 갔는데 5 정점은 이미 탐색 완료했네요?
그래서 막혔으니까 탐색 완료하고 9 정점에 10으로 종료타임 기록합니다.
다시 8로 왔는데 갈곳이 없으니까 여기도 탐색 완료하고 8 정점에 11로 종료타임 기록합니다.
이렇게 1의 이웃을 다 둘러봤으니 1은 탐색 끝났다고 보면되기 때문에 12로 종료타임 기록합니다.
다음은 새로운 정점 출발점인 13 정점을 봅시다.
13에서 갈 수 있는 화살표 이웃은 8 9 14입니다. 근데 8 9는 이미 종료 타임 기록했으니까 14만 갈 수 있네요.
14로 가봅시다. 정점 5는 이미 탐색했으니까 즉시 탐색 종료되고 15로 기록됩니다.
이렇게 13 정점도 이웃을 다 둘러봤으니 13 정점 탐색은 끝났다 보면되기 때문에 16으로 기록됩니다.
탐색 정리
1. (1|12) 정점에서 시작
2. (2|7) 정점으로 이동 (Tree Edge)
3. (3|4) 정점으로 이동 (Tree Edge)
4. (5|6) 정점으로 이동 (Tree Edge)
5. (8|11) 정점으로 이동 (Tree Edge)
6. (9|10) 정점으로 이동 (Tree Edge)
7. (13|16) 정점으로 이동, 새로운 시작점
8. (14|15) 정점으로 이동 (Tree Edge)
시간순으로 분류
각각 d[v]와 f[v] 값입니다.
1. (1 12) -> d[1] = 1 f[1] = 12 라는 식으로
2. (8 11)
3. (13 16)
4. (2 7)
5. (9 10)
6. (3 4)
7. (5 6)
8. (14 15)
그래프에 뭐 이상한 T B F C글자들이 있습니다. 이건 간선유형을 분류한겁니다.
각 간선의 유형은 다음과 같습니다 :
T (Tree Edge): DFS 트리를 구성하는 기본 간선
B (Back Edge): 현재 정점에서 조상 정점으로 돌아가는 간선
F (Forward Edge): 현재 정점에서 자손 정점으로 가는 간선
C (Cross Edge): 다른 DFS 트리 경로의 정점으로 가는 간선
DFS 시간 복잡도
Θ라는건 평균, 최악, 최선이 같다는거
Time = Θ(V+E)
- V는 정점(Vertex)의 수
- E는 간선(Edge)의 수
- 모든 정점과 간선을 반드시 한 번씩 방문하기 때문에 Θ임
DFS Forest (깊이 우선 숲)
1. 구조
- 하나 이상의 DFS 트리로 구성
- 각 트리는 연결되지 않은 컴포넌트를 나타냄
2. 트리 간선의 조건
- 간선 (u, v)에서:
u: 현재 탐색 중인 정점 (GRAY)
v: 아직 방문하지 않은 정점 (WHITE)
- 이런 조건의 간선만이 트리에 포함됨
3. 예시
그래프가 두 개의 컴포넌트로 나뉜 경우:
트리1: 트리2:
A E
/ \ |
B C F
|
D
이렇게 두 개의 독립된 DFS 트리가 모여 하나의 DFS Forest를 형성합니다.
괄호 정리 Parenthesis Theorem
모든 u와 v 정점은 다음의 조건중 하나에 만족합니다.
1. d[u] < f[u] < d[v] < f[v] 또는 d[v] < f[v] < d[u] < f[u]
따라서, u와 v는 Descendant(자손)관계가 성립하지 않습니다.
예: ( ) [ ] 처럼 서로 겹치지 않는 괄호
2. d[u] < d[v] < f[v] < d[u]
따라서, v는 u의 Descendant(자손)입니다.
예: ( [ ] ) 처럼 괄호가 포함되는 관계
3. d[v] < d[u] < f[u] < d[v]
따라서, u는 v의 Descendant(자손)입니다.
예: [ ( ) ] 처럼 괄호가 포함되는 관계
v가 u의 진짜 자손이 되는 조건은
d[u] < d[v] < f[v] < f[u] 일 때,
이는 DFS 트리에서 정점들의 관계를 시간값으로 판단할 수 있게 해줍니다.
White-path Theorem
u에서 v로 가는 Path가 모두 White Vertex로 이루어져있으면
v는 u의 Descendant(자손)입니다.
같은 말로
v는 u의 Descendant(자손)이면,
u에서 v로 가는 Path가 모두 White Vertex로 이루어져있습니다.
원래대로 해석하면, 2개의 명제 사이에 if and only if 라는 것이 들어가 있다.
필자가 한글로 해석하다 보니, 한글로 if and only if를 표현하기가 애매해서 위와 같이 나눠서 설명했다.
if and only if는 결국, 첫번째 명제가 T이면, 두번째 명제도 T 그리고
첫번째 명제가 F이면, 두번째 명제도 F임을 이야기한다.
[출처] 알고리즘) 22. Depth First Search|작성자 바보
간단하게 그냥 u에서 v까지 다 White Vertex면 v 정점은 u 정점의 자손이 됩니다.
DFS에서 트리의 간선 종류

위에서 트리 간선의 4가지 종류를 짧게 말했습니다.
더 자세히 보자면
1. Tree Edge (트리 간선)
- DFS 탐색 중 새로운(WHITE) 정점을 발견할 때 만드는 간선
- 예: u에서 미방문 정점 v를 처음 방문할 때 생기는 간선
2. Back Edge (후향 간선)
- 현재 정점(u)에서 자신의 조상 정점(v)으로 거슬러 올라가는 간선
- 예: 자식에서 부모로 돌아가는 간선
- White-path Theorem에 해당하기 때문에, Desendant인지 판단 가능합니다.
3. Forward Edge (전향 간선)
- 조상 정점(u)에서 자손 정점(v)으로 가는 "지름길" 간선
- Tree Edge가 아닌, 추가적인 경로를 제공하는 간선
4. Cross Edge (교차 간선)
- 같은 트리의 다른 가지나 다른 트리를 연결하는 간선
- 조상-자손 관계가 아닌 정점들 사이의 간선
무방향 그래프에서는 Tree Edge와 Back Edge만 존재합니다.
이는 무방향 그래프에서는 모든 간선이 양방향이므로,
Forward Edge와 Cross Edge가 자연스럽게 Tree Edge나 Back Edge로 해석되기 때문입니다.
따라서 무방향 그래프에서는 Tree > Back > Forward > Cross순으로 우선순위를 부여하면됩니다.
DFS 색 부여
간선 (u,v)를 만났을 때, v의 색상으로 간선 유형을 판단가능합니다.
v가 WHITE(미방문)일 때 Tree Edge, 처음 발견하는 새로운 경로입니다.
v가 GRAY(방문 중)일 때 Back Edge, 현재 탐색 중인 경로의 조상으로 돌아가는 간선입니다.
v가 BLACK(방문 완료)일 때 Forward Edge 또는 Cross Edge, 이미 탐색이 끝난 정점으로 가는 간선입니다.
'그냥 개발글 > 알고리즘' 카테고리의 다른 글
| 그래프 강한 결합 요소 Strongly Connected Components (0) | 2024.12.04 |
|---|---|
| 그래프 Topological Sort 알고리즘 (0) | 2024.12.03 |
| Elementary Graph Algorithms 기본 그래프 알고리즘 (0) | 2024.11.24 |
| Radix Sort 기수 정렬 (0) | 2024.10.20 |