
Strongly Connected Components, 줄여서 SCC라고 부릅니다.
강한 결합 요소 즉, SCC란 방향 그래프 G = ( V, E )에서 강하게 연결된 요소(SCC)는 그래프의 정점 집합 C ⊆ V 로,
이 집합의 모든 정점 u와 v에 대해 u에서 v로 가는 경로와 v에서 u가는 경로가 존재하는 최대 집합입니다.
뭔말인가요
C ⊆ V 는 C가 SCC랑 같은데, 이 SCC들이 V의 부분집합이어야한다는 말입니다.
즉 그래프의 정점들 중 일부로 구성된다는 것을 의미합니다.
u에서 v로 가는 경로와 v에서 u가는 경로가 존재한다는 말은 서로 상호 연결되서 u에서 v로 가고 v에서 u로 간다는 말입니다.
정점이 서로 도달 가능해야 강하게 연결된 요소,즉 SCC로 인정받을 수 있습니다.
최대 집합 또한 나오는데, "Maximal Set"이라는 용어로 해당 집합이 더 이상 다른 요소를 추가할 수 없는 상태라는 말입니다.
즉, 이 집합에 포함된 정점들끼리는 서로 연결되어 있지만, 다른 정점을 추가하면 연결성이 깨지게 됩니다.
말이 너무 어려운데 예시를 봅시다.

14 / 19 막 이런식으로 적혀있습니다만 이는 각각 시작 시간과 종료 시간인걸 보면 DFS가 된 그래프인걸 알 수 있죠?
DFS가 뭔지 모르시겠다면 아래 포스팅 보시면 됩니다.
https://kimyir.tistory.com/130
그래프 순회 BFS와 DFS
그래프 순회는 그래프 내의 정점을 한번씩 살펴보기 위해 방문하는 것입니다.이 순회에는 두 가지 BFS와 DFS 방식이 있습니다.BFS는 친구에게 소문 퍼지듯이 가까운 사람부터 탐색하는것이고,DFS는
kimyir.tistory.com
그리고 여기서 그룹으로 나눠서 테두리를 그려놨는데 이게 바로 SCC들입니다.
SCC 각각 보시면 서로 화살표로 상호연결되어있어 정점들끼리 가는 길이 존재합니다.
이걸 어렵게 말해서 집합 C에서 u와 v가 있다면 u~>v, v~>u로 가는 path가 있다고 합니다.
반대로 13/20에서 2/5로는 가지는데 2/5에서 13/20으로 가는길이 없는 경우는 서로 같은 SCC로 안묶이는걸 볼 수 있습니다.
각각 자기들끼리 연결되있는 상태에서 다른 정점을 추가하면 연결성이 끊어지기 때문에 각각 maximal한 상태,
즉 최대집합 상태입니다.
방향 그래프의 전치(Transpose) 형태
방향 그래프의 전치(Transpose) 형태,
즉 Transposed Form Of Directed Graph란 원래 그래프 G의 모든 간선의 방향을 반대로 뒤집은 것입니다.
간선의 방향이 뒤집어진 그래프 G^T 는 아래와 같이 정의됩니다.

이 그래프의 E^T 는 아래와 같습니다.

식이 이해가 안되는데 순서대로 설명하자면 E^T 간선 집합들이 중괄호 { 안에 들어가는 모든 쌍(u, v)를 포함한다는 말입니다.
이 모든 u에서 v로 가는 간선 쌍 (u, v)들에 대해서,
중간에 있는 : 기호는 "다음 조건을 만족하는" 이라는 의미입니다.
뒤에 (v, u) ∈ E는 원래 그래프 G 의 간선 집합 E에 (v, u)라는 간선이 존재한다는 의미입니다.
결론
E^T = {(u, v) : (v, u) ∈ E}는 "전치 그래프 G^T의 간선 집합 E^T는 원래 그래프 G의 간선 집합 E에서 (v, u)가 존재하는 모든 (u, v)쌍으로 구성된다"는 의미입니다.
원래 그래프 G와 전치 그래프 G^T는 동일한 강하게 연결된 요소(SCC)를 가집니다.
즉, 정점 u와 v가 G에서 서로 도달 가능하다면, G^T에서도 서로 도달 가능하다는 것을 의미합니다.
시간 복잡도
전치 그래프 G^T 는 인접 리스트를 사용하여
Θ( 𝑉 + 𝐸 ) 시간에 생성할 수 있습니다.
여기서 𝑉 는 정점의 수, 𝐸는 간선의 수를 의미합니다.
인접 리스트는 각 정점에 대해 그 정점과 연결된 다른 정점들의 리스트를 유지하는 데이터 구조입니다.
각 정점과 그에 연결된 간선을 모두 한 번씩 방문해야 하므로, 총 시간 복잡도는 정점 수와 간선 수의 합으로 표현됩니다.
컴포넌트 그래프 Component Graph
Strongly Connected Components에서 그룹들을 G^SCC, Component의 그래프로 부릅니다.

V^SCC = 각 SCC는 그래프의 정점으로 표현됩니다.
즉, 원래 그래프의 각 강하게 연결된 요소는 구성 그래프에서 하나의 정점으로 나타납니다.
E^SCC = 원래 그래프 G에서 두 SCC 간에 간선이 존재하면,
구성 그래프 G^SCC에서도 해당 SCC간에 간선이 추가됩니다.
SCC 그래프 예시
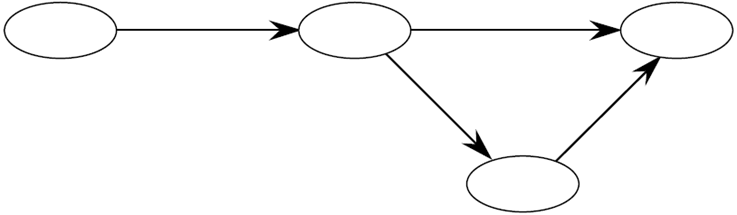


왼쪽 오른쪽 설명 모두 동일합니다.
다만 그냥 초점에 따라 다르게 설명한것뿐입니다.
전치 그래프 G^T에서 DFS를 수행할 때, 원래 그래프 G에서의 종료 시간에 따라 정점을 내림차순으로 방문하기 때문에 오른쪽 이미지에서 검은색 애들(종료순서)을 따라서 가라는거랑 같은 말입니다.

어쨋든 저 과정을 다시 한글로 옮겨보면
1. DFS(G) 호출:
원래 그래프 G에 대해 깊이 우선 탐색(DFS)을 수행하여 각 정점 u의 종료 시간을 f[u]로 기록합니다.
2. 전치 그래프 G^T 계산:
원래 그래프 G의 전치 그래프 G^T를 생성합니다. 전치 그래프는 모든 간선의 방향을 반대로 뒤집은 그래프입니다.
3. DFS(G^T) 호출:
전치 그래프 G^T에서 DFS를 수행합니다.
이때, 첫 번째 DFS에서 기록한 종료 시간을 기준으로 정점을 내림차순으로 방문합니다. 즉,
종료 시간이 높은 정점부터 낮은 정점 순으로 탐색합니다.
4. 출력:
두 번째 DFS에서 형성된 각 깊이 우선 탐색 트리의 정점들을 별도의 강하게 연결된 요소(SCC)로 출력합니다.
각 트리는 하나의 SCC를 나타냅니다.
G^SCC는 DAG다 Lemma
G^SCC는 DAG입니다. 즉, 구성 그래프는 방향성이 있으며, 사이클이 없는 그래프라는 의미입니다.
만약 v′ 에서 v로 가는 경로가 존재한다면, u, u′, v, v′ 를 포함하는 사이클이 형성됩니다.
이는 DAG의 정의에 어긋납니다.
다이어그램을 그려보면, v′ 에서 v로 가는 경로를 추가하면 u, u′, v, v′ 를 포함하는 원이 생긴다는 것입니다.
이는 사이클을 의미합니다.
SCC 정확성 증명
어떻게 SCC가 정확하단걸 증명할 수 있을까요?
아이디어는 다음과 같습니다.
두 번째 DFS에서 첫 번째 DFS의 종료 시간을 기준으로 내림차순으로 정점을 고려함으로써,
구성 그래프의 정점들을 위상 정렬(topological sort) 순서로 방문하고 있다는 것입니다.
즉, SCC를 찾는 과정이 올바르게 진행되고 있음을 나타냅니다
이 과정이 잘 작동하는지 증명하기 위해 두 가지 표기법 문제를 다루어야 합니다.
d[u]와 f[u]에 대해 논의할 때, 항상 첫 번째 DFS에 대한 값을 참조해야 한다는 점을 강조합니다.
즉, 두 번째 DFS를 수행할 때 이 값들을 참조해야 한다는 것입니다.
d(U): 집합 U에 속하는 정점들 중에서 가장 이른 발견 시간을 나타냅니다.
즉, U에 속하는 정점들 중에서 가장 먼저 방문된 정점의 발견 시간을 의미합니다.
f(U): 집합 U에 속하는 정점들 중에서 가장 늦게 종료된 시간을 나타냅니다.
즉, U에 속하는 정점들 중에서 가장 마지막에 탐색이 완료된 정점의 종료 시간을 의미합니다.
Lemma
C와 C ′는 그래프 G에서 서로 다른 강하게 연결된 요소(SCC)입니다.
만약 (u,v)라는 간선이 존재하고, u는 C에 속하며 v는 C′ 에 속한다고 가정합니다.

그러면 이런 그림이 나옵니다.
이 경우, f(C)>f(C′)라는 관계가 성립합니다.
즉, SCC C의 종료 시간은 SCC C′ 의 종료 시간보다 더 큽니다. 더 늦게 끝난다는거죠.
이 Lemma의 증명
(u, v) ∈ E^T 는 (v, u)∈E를 의미합니다.
즉, G와 전치그래프 G^T의 SCC는 동일하므로 f(C)>f(C′)가 성립합니다.
첫 번째 결과: 만약 C에서 C′로 가는 간선이 있다면,
C의 종료 시간이 C′ 보다 작아야 한다는 것을 의미합니다.
이는 탐색 순서와 종료 시간의 관계를 반영합니다.
두 번째 결과: 만약 C의 종료 시간이 C′ 보다 크다면,
C에서 C′ 로 가는 간선이 존재할 수 없다는 것입니다.
전치 그래프 G^T에서 두 번째 DFS를 수행할 때, 종료 시간이 최대인 SCC C에서 시작합니다.
즉, f(C)가 가장 큰 SCC를 선택합니다.
두 번째 DFS는 SCC C의 어떤 정점 x에서 시작하며, 이 정점에서 시작하여 C에 속하는 모든 정점을 방문합니다.
부수적 결과에 따르면, f(C)>f(C′)인 모든 다른 SCC C′ 에 대해 G^T에서 C에서 C′로 가는 간선이 존재하지 않습니다.
따라서, 두 번째 DFS는 오직 C에 속하는 정점만 방문하게 됩니다.
이는 DFS가 x에서 시작할 때, 깊이 우선 탐색 트리가 C의 정점들로만 구성된다는 것을 의미합니다.
'그냥 개발글 > 알고리즘' 카테고리의 다른 글
| 크루스칼 알고리즘 Kruskal’s Algorithm (0) | 2024.12.04 |
|---|---|
| 최소 신장 트리 Minimum Spanning Trees (0) | 2024.12.04 |
| 그래프 Topological Sort 알고리즘 (0) | 2024.12.03 |
| 그래프 순회 BFS와 DFS (0) | 2024.12.01 |