
이전 시간까지 Minimal Spanning Tree, 즉 MST를 구하는 기본적인 방법을 배워봤습니다.
이번엔 MST를 구하는 두 가지 방법 중 두 번째 프림 알고리즘을 배워볼겁니다.
- Kruskal’s Algorithm
- Prim’s Algorithm (오늘 배울거)
참고 : 가벼운 간선과 같은 용어를 모르신다면 MST를 공부하시면 됩니다.
https://kimyir.tistory.com/133
최소 신장 트리 Minimum Spanning Trees
최소 신장 트리(MST)를 이해하면 두 가지 주요 알고리즘인 크루스칼 알고리즘과 프림 알고리즘을 효과적으로 적용할 수 있습니다. 문제 정의한 마을에는 집과 도로가 있습니다.
kimyir.tistory.com

프림 알고리즘은 항상 하나의 트리를 구축합니다.
즉, 알고리즘이 진행되는 동안 항상 연결된 트리 구조를 유지합니다.
프림 알고리즘의 시작은 임의의 정점(루트)에서 시작합니다. 이 정점은 MST의 시작점이 됩니다.
이걸 r이라고 하겠습니다.
각 단계에서 MST에 포함된 정점 집합 V𝐴 와 포함되지 않은 정점 집합 V − V𝐴 사이의 "가벼운 간선(light edge)"을 찾습니다.
가벼운 간선은 MST에 추가할 수 있는 최소 가중치의 간선입니다.
선택된 가벼운 간선을 MST에 추가하고, 해당 간선에 연결된 정점을 MST에 포함시킵니다.
정리하자면
1. 현재 MST에 포함된 정점 집합 V𝐴 를 유지합니다.
2. V𝐴 와 V − V𝐴 사이의 가벼운 간선을 찾습니다.
3. 이 간선을 MST에 추가하고, 해당 간선에 연결된 정점을 V𝐴에 포함시킵니다.
4. 모든 정점이 MST에 포함될 때까지 이 과정을 반복합니다.
의사코드
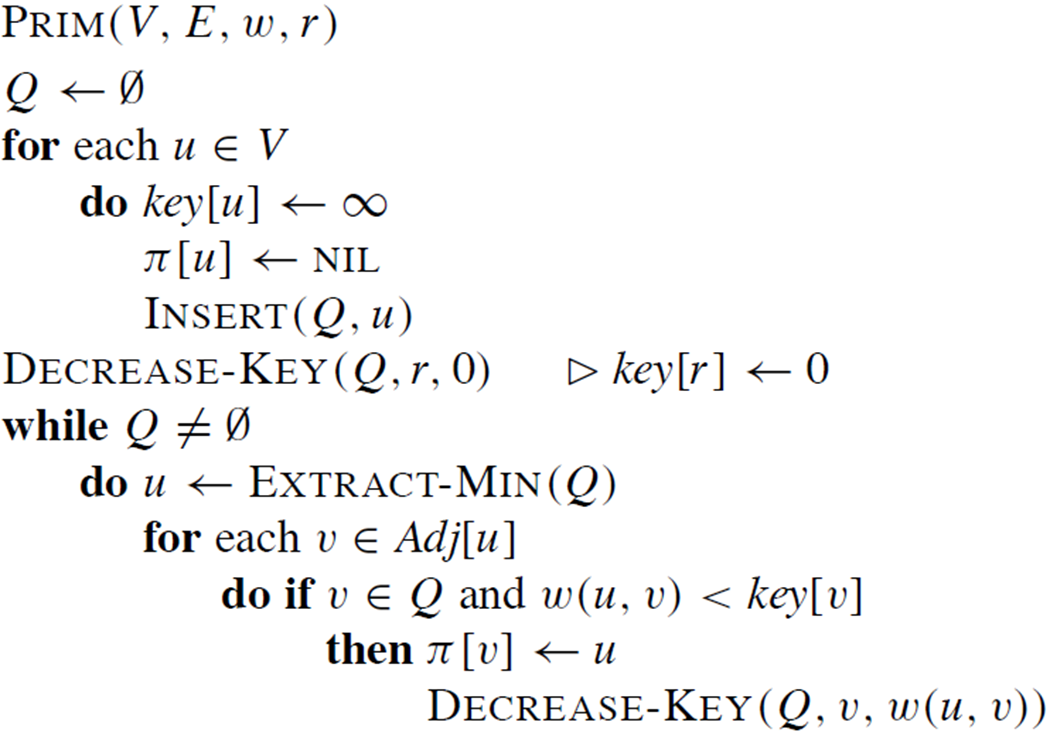
프림 알고리즘에서는 우선순위 큐(Q)를 사용하여 가벼운 간선을 효율적으로 찾습니다.
큐의 각 객체는 MST에 포함되지 않은 정점 V − V𝐴 에 들어있습니다.
각 정점 v의 키 값은 MST에 포함된 정점 u와의 간선 중 최소 가중치를 나타냅니다.
즉, u ∈ V𝐴 인 모든 간선 (u, v)의 최소 가중치입니다.
이 키 값은 해당 정점이 MST에 추가될 때의 가중치를 나타냅니다.
우선순위 큐에서 EXTRACT-MIN 연산을 수행하면, MST에 추가할 정점 v가 반환됩니다.
이 정점은 MST에 포함된 정점 V𝐴와 연결된 가벼운 간선을 가진 정점입니다.
만약 정점 v가 MST에 포함된 정점과 인접하지 않다면, 그 키 값은 무한대(∞)로 설정됩니다.
이는 해당 정점이 현재 MST에 추가될 수 없음을 나타냅니다.
다시 정리하자면
알고리즘의 입력으로 주어진 루트 정점 r에서 시작합니다. 이 정점은 MST의 시작점이 됩니다.
r는 알고리즘에 입력으로 주어지지만, 임의의 정점이 될 수 있습니다.
각 정점은 트리에서 자신의 부모를 알고 있습니다. 이 정보는 π[v]라는 속성으로 저장됩니다.
π[v]는 정점 v의 부모를 나타내며, 루트 정점 r의 경우 π[v]=NIL로 설정됩니다.
이는 루트 정점이 부모가 없음을 의미합니다.
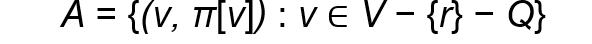
해당 공식은 알고리즘 진행되면서 MST에 포함되지 않은 정점 집합 V−{r}−Q에 대해 각 정점과 그 부모 정보를 저장합니다.
알고리즘이 종료되면, V𝐴 = V가 되고 Q = ∅이 됩니다. 큐가 비게 됩니다. 즉, 모든 정점이 MST에 포함됩니다.
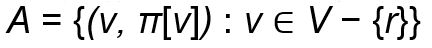
결국 MST는 이렇게 표현됩니다.
시간 복잡도

시간 복잡도는 우선순위 큐가 어떻게 구현되었는지에 따라 달라집니다. 이진 힙(binary heap)을 사용한다고 가정합시다.
우선순위 큐 Q를 초기화하고 첫 번째 for 루프를 수행하는 데 필요한 시간 복잡도는 O(V log V)입니다.
여기서 V는 정점의 수입니다.
루트 정점 r의 키 값을 감소시키는 데 필요한 시간 복잡도는 O(log V)입니다.
|V|번의 EXTRACT-MIN 호출이 필요하므로, 이 부분의 시간 복잡도는 O(V log V)입니다.
간선의 수 |E|에 비례하여 DECREASE-KEY 호출이 발생하므로, 이 부분의 시간 복잡도는 O(E log V)입니다.
결국 다 더하면 O(V log V)+O(E log V)가 되지만, 일반적으로 |E|가 |V|² O(E logV)가 더 지배적인 항이 됩니다.
이 내용은 전포스팅 크루스칼 알고리즘에서도 다뤘습니다. 따라서 O(V log V)는 생략해도 됩니다.
결론적으로 프림알고리즘의 시간복잡도는 O(E log V) 입니다.
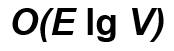
크루스칼 알고리즘 vs 프림 알고리즘
크루스칼 알고리즘:
간선 중심의 접근 방식입니다.
모든 간선을 가중치에 따라 정렬한 후, 가장 낮은 가중치의 간선부터 선택하여 MST에 추가합니다.
사이클을 형성하지 않도록 유니온-파인드 자료구조를 사용하여 간선을 선택합니다.
프림 알고리즘:
정점 중심의 접근 방식입니다.
임의의 정점에서 시작하여 MST에 포함된 정점과 포함되지 않은 정점 사이의 가벼운 간선을 선택하여 MST를 확장합니다.
현재 MST에 연결된 정점과 연결되지 않은 정점 사이의 최소 가중치 간선을 선택합니다.
부록
만약 경로의 weight, 가중치가 마이너스라면 알고리즘이 작동할까요?
네 그래도 알고리즘이 작동됩니다.
'그냥 개발글 > 알고리즘' 카테고리의 다른 글
| 그래프 알고리즘 시간 복잡도 총정리 (0) | 2024.12.09 |
|---|---|
| 최단경로 Shortest-Paths 알고리즘 (0) | 2024.12.04 |
| 크루스칼 알고리즘 Kruskal’s Algorithm (0) | 2024.12.04 |
| 최소 신장 트리 Minimum Spanning Trees (0) | 2024.12.04 |