
최소 신장 트리(MST)를 이해하면 두 가지 주요 알고리즘인 크루스칼 알고리즘과 프림 알고리즘을 효과적으로 적용할 수 있습니다.
문제 정의
한 마을에는 집과 도로가 있습니다.
각 도로는 두개의 집만 연결합니다.
두 집 House u와 House v를 연결하는 도로의 수리 비용은 w(u,v)입니다.
목표
모든 집이 서로 연결되도록 충분한 도로를 수리하되, 수리 비용이 최소가 되도록 해야 합니다.
즉, 모든 집이 서로 도달 가능해야 하며, 총 수리 비용이 최소화되어야 합니다.
그래프 정의
- 비방향 그래프 로 구성되어 있습니다.
- : 정점(집)
- : 간선(도로)
각 간선 (u,v)에 대해 가중치 w(u,v)가 정의되어 있습니다.
이는 도로의 수리 비용을 나타냅니다.
목표
T⊆E 를 찾아야 합니다.
1. T는 모든 정점을 연결해야 하며, T는 신장 트리(spanning tree)입니다.
2.

이 식이 최소화되어야 합니다.
즉, 선택된 간선(u, v)쌍의 총 가중치(비용)가 최소가 되어야 합니다.
정리하자면 모든 신장 트리 중에서 가중치가 최소인 신장 트리를 최소 신장 트리(MST)라고 합니다.
예시

사진에 보시다시피 회색으로 칠해진 간선들은 모든 정점을 연결하면서도 총 가중치가 최소인 간선들입니다.
이 간선들이 바로 Minimum Spanning Tree, 즉 MST입니다.
하나의 그래프에 여러 개의 MST가 존재할 수 있습니다.
예를 들어, MST 간선 (e,f)를 그냥 간선 (c,e)로 교체하면, 새로운 다른 신장 트리 MST`가 생성되지만 가중치는 동일합니다.
MST의 속성
간선 수: MST는 | V | − 1개의 간선을 가집니다. (여기서 |V|는 정점의 수), 트리이기 때문에 간단히 생각하면됩니다.
즉, 모든 정점을 연결하면서도 최소한의 간선만 사용합니다.
사이클 없음: MST는 사이클을 포함하지 않습니다. No Cycle.
비방향이기 때문에 사이클이 존재할 수가 없습니다.
유일하지 않을 수 있음: MST는 여러 개 존재할 수 있습니다. 다른 MST`가 존재가능한거죠.
MST 구하는 법
1. 간선의 집합 A를 구축합니다. 처음에는 A에 간선이 없습니다.
2. 루프 불변 조건: 반복문으로 간선을 A에 추가할 때마다 "A는 어떤 MST의 부분 집합이다"라는 조건을 유지해야 합니다.
즉, 추가하는 간선이 MST의 일부가 될 수 있어야 합니다. 루프 불변이니 반복문의 참인 조건이죠.
3. 간선 (u,v)가 A에 추가될 때, A가 어떤 MST의 부분 집합이여야합니다. 이를 위해 안전한 간선만 추가합니다.
즉, 이 과정을 정리한 식은 A∪{(u,v)}인데, 이 집합 A가 어떤 MST의 부분 집합이 되어야 한단겁니다.
MST 구하는 의사 코드

입력: 인자로 각각 그래프 G와 각 간선의 가중치 w를 받습니다.
출력: 최소 신장 트리 A
과정을 보자면
초기화: A를 빈 집합으로 설정합니다.
반복문: A가 신장 트리가 아닐 때까지 반복합니다. 안전한 간선(u, v)을 찾아서 A에 추가합니다.
결과 반환: 최종적으로 A를 반환합니다.
몇가지 개념 정의
S ⊂ V, A ⊆ E라고 가정하도록합시다.
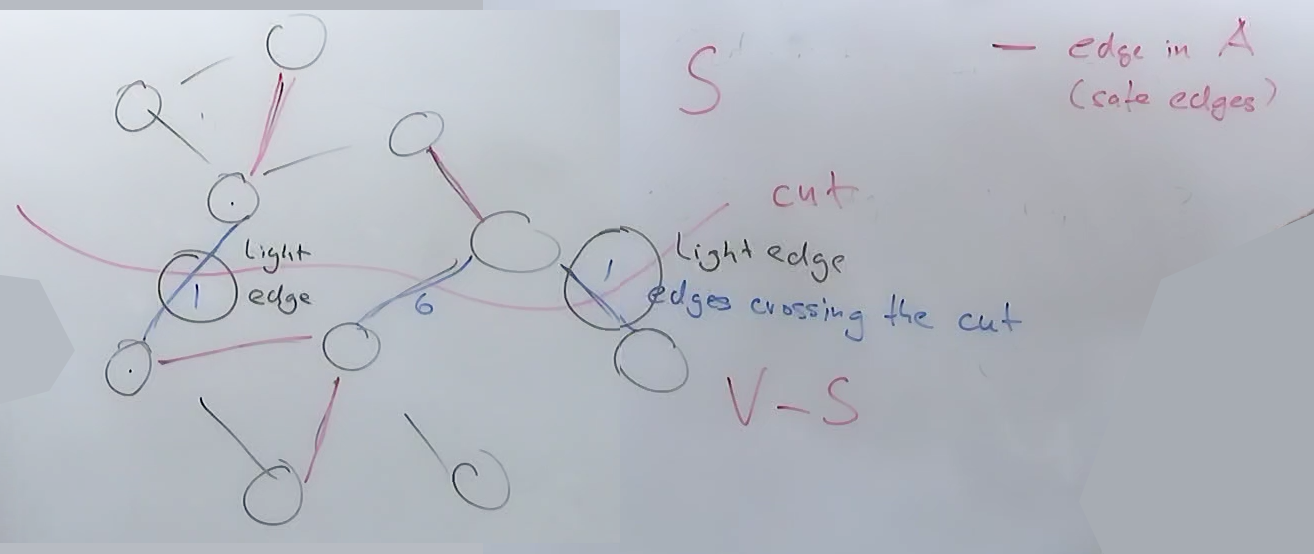
Cut : 그래프의 집합 V를 S 집합과 V−S 집합으로 정점을 나누는 파티션입니다.
사진에서는 그냥 반으로 S 집합과 V - S 집합으로 나눴습니다.
Cross : 간선 (u,v)가 컷 (S, V−S)를 교차한다고 할 때,
u의 한 끝점이 S에 있고, 다른 끝점 v가 V−S에 있을 때 그 간선이 크로스하고 있다고 합니다.
사진에서는 파란선들이 Cut에 덮여있으니 이 간선들이 Cross입니다.
Respects : 컷이 집합 A를 존중한다고 할 때, A의 어떤 간선도 컷을 교차하지 않는 경우를 의미합니다.
다시 말하자면 안전한 간선이란 MST에 포함가능한 간선입니다.
즉, 모든 간선 중에서 가중치가 가장 낮은 간선입니다.
그리고 집합 A에 들어가는 간선들은 모두 안전한 간선들만 들어갑니다.
이 때 집합 A의 간선들이 Cross 하는 간선들이 아니라면 컷이 집합 A를 존중한다고 하는겁니다.
이게 왜 필요하냐면 컷을 나누는 과정에서 집합 A의 간선이 포함되지 않도록 하는 조건을 위해섭니다.
Light Edge : 컷을 교차하는 간선 중에서 가중치가 최소인 간선을 의미합니다.
즉, 주어진 컷을 교차하는 모든 간선 중에서 가장 가벼운 간선입니다. 하나의 컷에 여러 Light Edge가 존재 가능합니다.
Respects와 다르게 컷을 교차하는, 즉 컷을 지나는 간선만 해당됩니다. 그중에서 가중치가 가장 낮은 간선이죠.
위 이미지에서의 세 파란 Cross 간선 중 왼쪽부터 3 6 1이라면 가장 오른쪽의 파란 cross 간선이 Light Edge,
이미지처럼 1 6 1이라면 두 1 간선들이 모두 Light Edge입니다.
이 Light Edge는 굉장히 중요합니다. 반복적으로 Light Edge만 찾다보면 MST가 완성되기 때문입니다.
아래 중심 정리에서 설명드리겠습니다.
중심정리 Central Theorem
1. 집합 A가 어떤 MST의 부분 집합이라고 가정합니다.
2. (S, V−S)는 집합 A를 존중하는 컷입니다.
3. (u, v)는 컷 (S, V−S)를 가로지르는 라이트 엣지입니다.
4. 그러면 (u, v)는 집합 A에 대해 안전한 간선입니다.
증명 과정
이 중심정리를 한번 정리해봅시다. (u,v)가 안전한 간선이라는 것을 보여주는 것이 목표입니다.
T를 집합 A를 포함하는 MST라고 가정합니다.
(a) 만약 T가 (u,v)를 포함한다면, 증명이 완료됩니다.
(u, v)가 안전한 간선이니까 MST에 포함되는겁니다.
(b) 만약 T가 (u,v)를 포함하지 않는다면, 이제 좀 어려워집니다.
방식은 A와 {(u,v)}를 포함하는 다른 MST′ 를 구성하는겁니다.
일단 b의 상황을 봅시다.
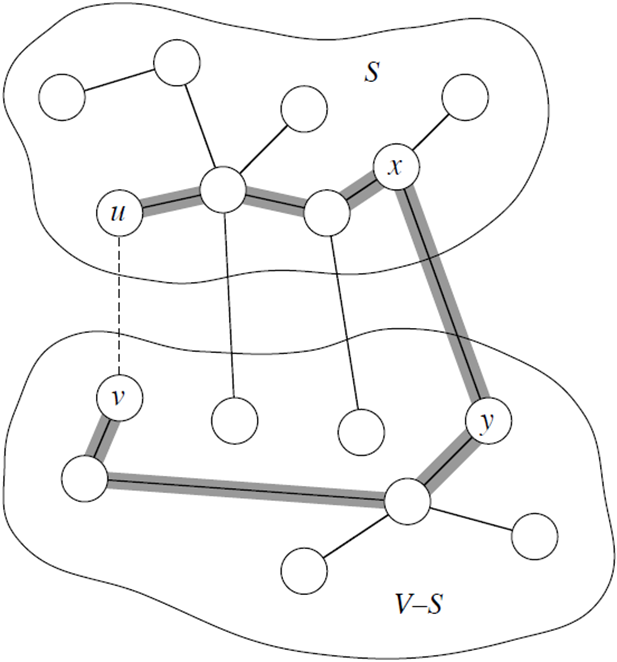
트리에서는 각 정점 쌍 사이에 유일한 경로가 존재합니다. 즉, 두 정점 u와 v 사이에는 오직 하나의 경로만 있습니다.
지금 사진엔 u와 v 사이가 실선으로 되어있는데 아직은 u와 v가 연결안되어있어요. 간선 (u, v)는 연결안되어있습니다.
T가 MST이므로, u와 v 사이에 유일한 경로 p가 존재합니다.
이 경로는 컷 (S, V−S)를 최소한 한 번은 가로질러야 합니다.
경로라는게 중요합니다. 여러 간선들이 구성되는 경로입니다.
경로 p의 엣지 중 하나를 (x, y)라고 할 때, 이 엣지는 컷을 가로지릅니다. 사진에서는 회색선에 진한 검은색 선 보이시죠?
(u, v)를 선택할 때, 이 엣지의 가중치는 w(u, v)로 표현됩니다. 그리고 (x, y)의 가중치는 w(x, y)로 표현됩니다.
따라서, w(u, v) ≤ w(x, y)가 성립해야 합니다. 이는 (u, v)가 라이트 엣지라는 정의와 일치합니다.
웬 대소비교가 나오냐면 우리가 지금 MST를 찾아내야하기 때문에 u와 v의 간선은 무조건 가중치가 젤 낮겠죠?
만약 w(u, v)가 더 크다면 굳이 이걸 고를 필요없이 (x, y)을 골랐겠죠.
컷이 집합 A를 존중하므로, 엣지 (x, y)는 집합 A에 포함되지 않습니다.
즉, (x, y)는 컷을 가로지르지만, 집합 A에는 속하지 않는 간선입니다.
이번엔 아까 말했던 새로운 트리 T' 를 만들어봅시다.
우선 기존 MST T에서 (x, y)를 제거하여 두 개의 컴포넌트로 나눕니다.
그런 다음, 간선 (u, v)를 추가하여 두 컴포넌트를 다시 연결합니다.
이 때 기존 MST w(T) ≥ MST w(T)' 가 만족됩니다.
왜냐면 w(u, v) ≤ w(x, y)가 성립되기 때문에 우린 u, v를 라이트 엣지로 설정했으니까
당연히 기존 (x, y) 간선을 연결한 w(T)가 더 크거나 같은거죠. 증명 끝.
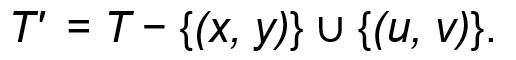
이제 이 공식을 봅시다.
새로운 MST T'는 기존 T 에서 (x, y) 간선을 빼기, 즉 제거한 뒤 (u, v)를 합집합, 즉 (u, v)를 추가한겁니다.
결국 T′ 는 스패닝 트리입니다. 모든 정점을 포함하고 연결되어 있기 때문입니다.
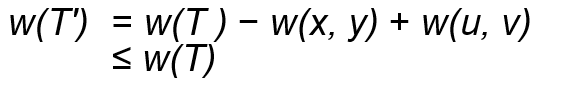
가중치 공식도 봅시다.
새로운 MST T'는 기존 T의 가중치 - 간선(x, y)을 제거했으니 가중치를 빼줍니다.
그리고 새로운 간선 w(u, v)를 추가했으니 가중치를 더해줍니다.
이 가중치의 결과물이 바로 MST T'의 가중치입니다.
w(T') ≤ w(T)는 위에 증명에서 말했듯이 라이트 엣지 때문에 무조건 라이트 엣지 (u, v)를 가진 T' 가 더 작거나 같습니다.
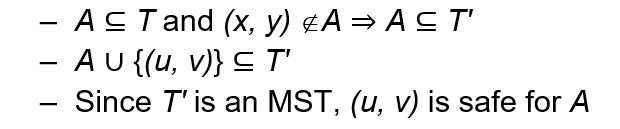
마지막으로 (u, v)가 집합 A에 대해 안전한 간선임을 보여야 합니다.
집합 A가 기존 MST T에 포함되고, 간선 (x, y)가 A에 포함되지 않으므로, A는 새로운 MST T′에도 포함됩니다.
그리고 A와 (u, v)를 합친 집합이 새로운 MST T′ 에 포함됩니다.
새로운 MST T′ 가 MST이므로, (u, v)는 안전한 간선으로 인정받습니다.
즉, (u, v)가 MST에 포함될 수 있음을 의미합니다.
부록

C는 그래프 G 𝐴 의 연결된 컴포넌트를 나타냅니다.
여기서 G 𝐴 는 정점 집합 V와 간선 집합 A로 구성된 그래프입니다.
만약 (u, v)가 컴포넌트 C와 G 𝐴 의 다른 컴포넌트와 연결되는 라이트 엣지라면, 컷 (V𝐶, V − V𝐶)를 가로지르는 간선일겁니다.
이 때 (u, v)는 집합 A에 대해 안전하다는 것입니다.
즉, 이 간선은 MST에 포함될 수 있습니다.
갑자기 든 생각이지만 만약 Minimum Spanning Tree가 아닌 Maximum Spanning Tree를 구하려고 하면 어떻게 될까요?
Light Edge : 컷을 교차하는 간선 중에서 가중치가 최소인 간선을 의미합니다.
이 정의를 거꾸로 해서 최소가 아닌 최대인 간선을 찾는것으로 바꾸면 다 반대가 되기 때문에 구할 수 있겠죠?
어쨋든 오늘 알아본 MST의 아이디어로 뒤에 설명할 Kruskal Algorithm에 사용됩니다. 다음 포스팅에 다시 다뤄봅시다.
'그냥 개발글 > 알고리즘' 카테고리의 다른 글
| 프림 알고리즘 Prim’s Algorithm (0) | 2024.12.04 |
|---|---|
| 크루스칼 알고리즘 Kruskal’s Algorithm (0) | 2024.12.04 |
| 그래프 강한 결합 요소 Strongly Connected Components (0) | 2024.12.04 |
| 그래프 Topological Sort 알고리즘 (0) | 2024.12.03 |