지수 기호 복붙
2⁰¹²³⁴⁵⁶⁷⁸⁹
이전에 순차 탐색 알고리즘과 이진 탐색 알고리즘을 시간 복잡도 함수 T(n)으로 나타냈었다.
여기서 T(n)의 T는 time complexity를 줄임말이다.
그런데 이진 탐색 알고리즘의 T(n) = k+1 함수에서 1이라는 오차를 신경 쓰지 않고
오히려 제외하여 k만을 구하여 T(n)=log2n 이라는 식을 얻었다.
그런데 과연 이 오차가 1이 아닌 1000000과 같이 더 큰 수라면 어떻게 될까?
이럴 때 필요한 것이 빅 - 오만 따지는 것이다.
빅 - 오란 말 그대로 함수 T(n)에서 영향력이 가장 큰 부분을 따진 것이다.
영향력이 크기에 O가 매우 크다는 뜻에서 빅 - 오인 것이다.
#1 빅 - 오 예시
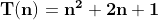
위의 식에서 각 항이 수가 늘어남에 따라 차지 하는 비율을 표로 작성해보자

표에서 알 수 있듯 식에서 최고차항인 n^2이 수가 늘어날 수록
차지하는 비율이 점점 커진다는 사실을 알 수 있다.
따라서 사실상 n² 빼고 다 간략화 시키면

으로 남게 되고, 이를 빅 - 오 표기법으로 표현하자면

읽을 땐 "Big-Oh of n^2"이라 읽는다
이는 n의 증가 및 감소에 따른 T(n)의 변화 정도가 n² 형태를 띤다는 것이다.
이렇게 단순하게 빅 - 오를 구하는 방법은 다음과 같다.
"T(n)이 다항식으로 표현이 된 경우, 최고차항의 차수가 빅 - 오가 된다"
이를 일반화하여 나타내면

이렇게 데이터 수의 증가에 따른 연산 횟수의 증가 형태를 표현한 것이 빅 - 오 이기 때문에 대표적인 유형들이 있다.
#2 빅 - 오의 대표적인 유형들

여기서 주의깊게 봐야할 것은 O(log n) 정도는 되야 쓸만한 알고리즘이라는 것이다.
따라서 나중에 O(log n) 이상의 빅오를 띠는 알고리즘은 최대한 줄여야할 필요가 있다.
1 (constant): growth is independent of the problem size n.
log2N (logarithmic): growth increases slowly compared to the problem size (binary search)
N (linear): directly proportional to the size of the problem.
N * log2N (n log n): typical of some divide and conquer approaches (merge sort)
N2 (quadratic): typical in nested loops
N3 (cubic): more nested loops
2N (exponential): growth is extremely rapid and possibly impractical.
#3 빅 - 오에 대한 수학적 접근
우선 수학적 정의부터 살펴보자
"두 개의 함수 f(n)과 g(n)이 주어졌을 때, 모든 n ≥ K에 대하여
f(n) ≤ C g(n) 을 만족하는 두 개의 상수C와 K가 존재한다면
f(n)의 빅-오는 O(g(n))이다."
이 부분 부터는 이해하기 위해 쓴 것이라 정확한 정보가 아닐 수 있습니다.
이제 다음 두 함수를 비교해보자
- f(n) = 5n² + 100
- g(n) = n²
우선 n ≥ K 에서 K를 대략 12 정도로 선택하고, 이 상황에서 f(n) ≤ C g(n) 을 만족 시키기 위한 상수 C를 생각해보자
이 때 C는 크든 작든 상관없다. 그러므로 크게 1000 정도로 잡아보면 f(n) ≤ C g(n) <= C = 1000
각 함수 식을 그대로 정리해보면
5n² + 100 ≤ 1000n²
즉, 빅-오 정의에 해당하는 C = 1000, K = 12인 경우가 존재하므로
f(n)의 빅-오는 O(n²) 이다. == 5n² + 100의 빅-오는 O(n²) 이다.
이해가 안되면 위에 수학적 정의를 보면서 다시 비교를 해보자
실제로 그래프 그려보면 K가 12 아니여도 1000n² 의 기울기는 엄청 가파르다.
때문에 대충 K가 2여도 저 식이 성립한다.
그러면 위에처럼 과연 상수 C와 K를 마음대로 크게 어림 잡아도 되는걸까?
먼저 K의 값의 역할은 n ≥ K 으로 식의 범위 제한을 둔 것이다.
n은 어쨋든 계속 커지고, 그러다 어느 순간 이후부턴 f(n) ≤ C g(n) 을 만족할 것이다.
때문에 n의 값 자체는 사실 빅 - 오를 판단할 땐 딱히 중요하지않다.
중요한 것은 n의 값이 계속 커지면서 어느 순간 부터 항상 f(n) ≤ C g(n) 을 만족한다는 사실이다.
그러면 상수 C는 크게 잡아도 상관 없을까?
이는 이미 얘기한 것처럼
"5n² + 100의 빅 - 오는 O(n²) 이다."
빅 - 오는 증가율의 상한선을 표현하는 표기법이므로 n² 의 증가율 패턴을 보이기만 하면되니깐 C가 커도 상관없는 것이다.
앞서 수학적 정의에서 n은 데이터 수이고 연산횟수는 0이상이기에 n ≥ 0 , f(n) ≥ 0, g(n) ≥ 0 이라는 조건은 필수이다.
'그냥 개발글 > 자료구조 이론' 카테고리의 다른 글
| 2-2 재귀함수의 활용 (0) | 2023.01.07 |
|---|---|
| 2-1 함수의 재귀적 호출 (0) | 2023.01.05 |
| 1-3 순차 탐색 알고리즘과 이진 탐색 알고리즘 (0) | 2022.08.05 |
| 1-2 알고리즘 성능분석 (0) | 2022.08.05 |