이전에 재귀함수 특징을 알아보았다.
재귀함수는 이해하는 것도 중요하지만 잘 정의하는 것도 중요하다.
함수끼리의 호출 순서보단 함수끼리의 호출 관계를 더 잘 살펴보면서 연습을 하도록하자
#1 파보나치 수열
파보나치 수열은 대표적인 재귀 형태의 수열로서 다음과 같이 전개된다.
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, 55 · · · ·
앞에 두 숫자 더해서 현재의 수를 만들어가는 수의 나열이라고 보면된다.
때문에 0 + 1 은 1이므로 0과 1이 해당하는 첫번 째 두번 째 인덱스 값은 고정이다.

고등학교 때 확통에서 제대로 배우기 전에 수학 쌤이 재미로 칠판에 그렸던 기억이....
이러한 파보나치 수열의 규칙은 다음과 같이 표현된다.
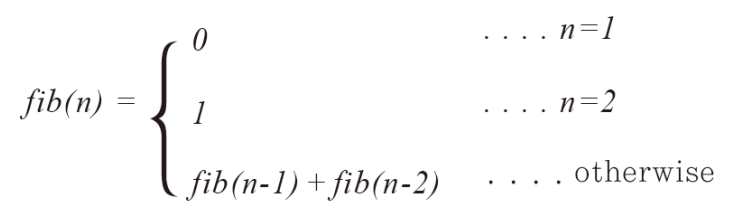
이를 코드로 옮겨보면
#include <stdio.h>
int Fibo(int n)
{
if (n == 1)
return 0;
else if (n == 2)
return 1;
else
return Fibo(n - 1) + Fibo(n - 2);
}
int main(void)
{
int i;
for (i = 1; i < 15; i++)
printf("%d ", Fibo(i));
return 0;
}
위 코드에서 Fibo(n - 1) + Fibo(n - 2); 이부분은
왼쪽의 Fibo(n - 1)이 먼저 호출완료 되어야 오른쪽이 호출되기에
다음과 같은 순서로 작동하게된다.

앞서 말했듯이 함수의 호출 순서보단 관계에 더 집중하라고 했었는데
이는 재귀함수가 매우 많은 수의 함수들이 위의 그림처럼
호출이 되기 때문에 순서를 알기 힘들기 때문이다.
#2 이진 탐색 알고리즘을 재귀적으로 구현
이전에 이진 탐색 알고리즘을 코드로 구현했을 땐
그저 while문으로 first와 last 인덱스 번호가 역전될 때까지 탐색하였다.
그런데 그 while문의 반복 패턴을 재귀 함수로 구현 가능하다.
아래는 탐색 대상 배열, 첫 인덱스, 마지막 인덱스, 탐색 대상을 인자로 받는 재귀함수다.
#include <stdio.h>
int BSearchRecur(int ar[], int first, int last, int target)
{
int mid;
if (first > last)
return -1; // -1의 반환은 탐색의 실패를 의미
mid = (first + last) / 2; // 탐색대상의 중앙을 찾는다.
if (ar[mid] == target)
return mid; // 검색된 타겟의 인덱스 값 반환
else if (target < ar[mid])
return BSearchRecur(ar, first, mid - 1, target);
else
return BSearchRecur(ar, mid + 1, last, target);
}
int main(void)
{
int arr[] = {1, 3, 5, 7, 9};
int idx;
idx = BSearchRecur(arr, 0, sizeof(arr) / sizeof(int) - 1, 7);
if (idx == -1)
printf("탐색 실패 \n");
else
printf("타겟 저장 인덱스: %d \n", idx);
idx = BSearchRecur(arr, 0, sizeof(arr) / sizeof(int) - 1, 2);
if (idx == -1)
printf("탐색 실패 \n");
else
printf("타겟 저장 인덱스: %d \n", idx);
return 0;
}-1이 나오면 탐색 실패로 나타 내고
이외에는 탐색 대상을 찾을 때 까지 반으로 쪼개어 방향 찾아서
그 방향의 구간을 또 반복하여 찾는걸
재귀함수로 나타낼 수 있다.
'그냥 개발글 > 자료구조 이론' 카테고리의 다른 글
| 3-1 추상 자료형 (0) | 2023.01.09 |
|---|---|
| 2-3 재귀의 활용 - 하노이 타워 (0) | 2023.01.07 |
| 2-1 함수의 재귀적 호출 (0) | 2023.01.05 |
| 1-4 빅-오 표기법 (Big-Oh Notation) (0) | 2023.01.03 |