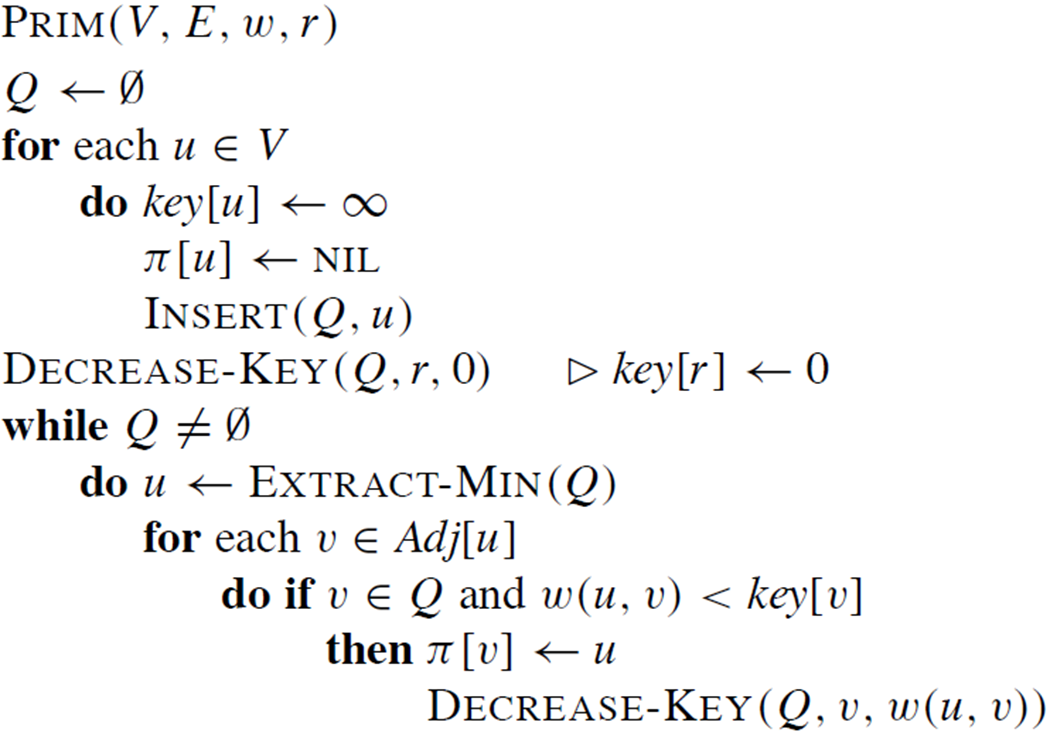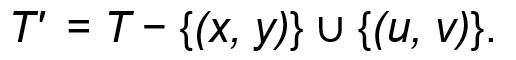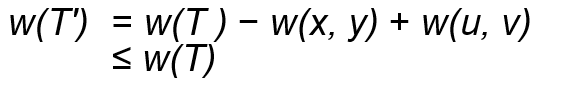문제 정의

두 점 사이의 최단 경로를 찾는 방법

입력

방향 그래프 G = (V, E)
가중치 함수 w : E → R

경로의 가중치 : 경로 p = <v0, v1, …, vk>의 가중치는 경로에 있는 모든 간선의 가중치의 합으로 정의됩니다.

즉 w(p) = w(v0, v1) + w(v1 + v2) + ... + w(vk-1, vk)이런식으로 더하면 됩니다.
기존 경로의 가중치를 구할 땐 경로의 Weight w(p)는 경로 사이에 존재하는 모든 간선의 Weight의 합입니다.

최단 경로 가중치 : 두 정점 u와 v 사이의 최단 경로 가중치는 다음과 같이 정의됩니다.

여기서 w(p)는 경로 p의 가중치입니다.

min으로 u에서 v로 가는 모든 경로 p 중에서 가중치가 가장 작은 경로를 찾습니다.

만약 u에서 v로 가는 경로가 없다면, 최단 경로 가중치는 무한대(∞)로 설정됩니다. 이는 도달할 수 없는 경로를 나타냅니다.

u에서 v까지의 최단 경로는 w(p)=δ(u,v)를 만족하는 모든 경로 p입니다.

예시

해당 예시에서는 BFS로 적용된 weight가 그래프에 보여집니다.

예시에서 최단 경로가 유일하지 않을 수 있음을 보여줍니다. 즉, 여러 경로가 동일한 최단 가중치를 가질 수 있습니다.

한 정점에서 다른 모든 정점으로 가는 최단 경로를 고려할 때, 이 경로들이 트리 구조로 조직된다는 점을 강조합니다. 

이는 최단 경로 트리(Shortest Path Tree)라고 불립니다.

예를 들면 s에서 y로 가는 최단 경로가 s → y라면, y에서 다른 정점으로 가는 최단 경로도 s를 기준으로 연결됩니다.
이와 같은 방식으로 모든 정점이 s로부터의 최단 경로를 통해 연결되면, 최단 경로 트리가 형성됩니다.

최단 경로 문제들 

Single-source : 주어진 출발 정점 s에서 모든 정점 v로 가는 최단 경로를 찾는 문제입니다.
Single-destination : 주어진 목적지 정점으로 가는 최단 경로를 찾는 문제입니다.
Single-pair : 두 정점 u와 v 사이의 최단 경로를 찾는 문제입니다.
이 경우, 최악의 경우에 대해 Single-source 문제를 해결하는 것보다 더 나은 방법이 알려져 있지 않습니다.

즉, 두 정점 간의 최단 경로를 찾기 위해 Single-source 문제를 해결하는 것이 최악의 경우에도 가장 좋은 방법이라는 것입니다.

All-pairs : 모든 정점 u와 v 쌍에 대해 최단 경로를 찾는 문제입니다.

음수 가중치 간선

출발점에서 도달할 수 없는 음수 가중치 사이클이 있는 경우에는 문제가 없습니다. 

즉, 이 사이클에 도달할 수 없다면 최단 경로 계산에 영향을 미치지 않습니다.

하지만 만약 음수 가중치 사이클이 존재하고, 이 사이클을 계속 돌 수 있다면, 최단 경로의 가중치는 무한히 작아질 수 있습니다. 
즉, w(s, v) = −∞가 되어, 사이클에 포함된 모든 정점 v에 대해 최단 경로 가중치가 무한히 작아질 수 있습니다.

경로의 가중치는 경로에 있는 모든 간선의 가중치의 합이기 때문입니다.

일부 최단 경로 알고리즘은 그래프에 음수 가중치 간선이 없을 때만 작동합니다. 

음수 가중치 간선이 존재하면 알고리즘의 결과가 신뢰할 수 없게 될 수 있습니다.

정리 Lemma

최단 경로의 모든 부분 경로는 최단 경로라는 것입니다. 

즉, 최단 경로의 일부를 잘라내어도 여전히 최단 경로가 유지된다는 의미입니다.

증명 Proof

잘라내기 및 붙이기 기법 (Cut-and-paste technique)을 사용하여 증명합니다.

우선 경로의 가중치 총합은 다음과 같습니다.

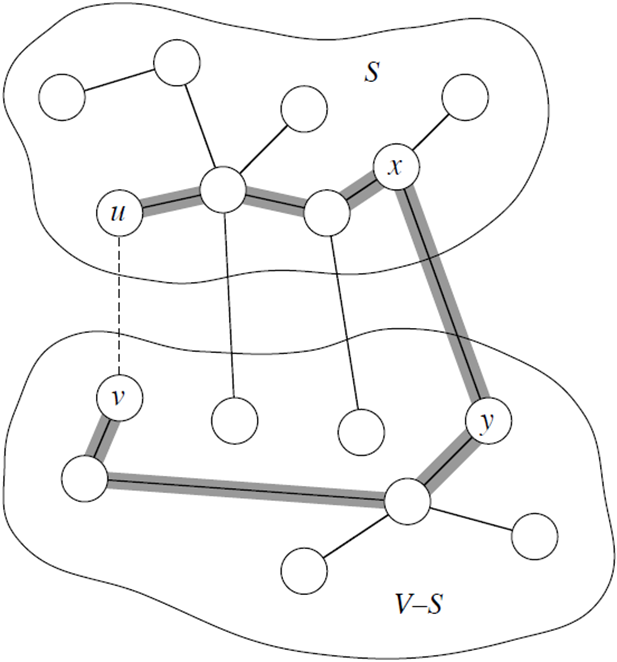
Shortest Path(u, v) = w(p) = w( p𝑢𝑥 ) + w( p𝑥𝑦 ) + w( p𝑦𝑣 )

정점 u에서 v까지의 최단 경로를 p𝑢𝑥 (u에서 x까지), p𝑥𝑦 (x에서 y까지), p𝑦𝑣 (y에서 v까지)로 나누어 설명합니다.
만약 x에서 y까지의 경로가 p𝑥𝑦 보다 짧다고 가정하면, 전체 경로 p𝑢𝑥와 p𝑦𝑣 를 포함한 경로가 더 짧아질 수 있습니다.

즉, w( p'𝑥𝑦 ) < w( p𝑥𝑦 )

그렇게 되면 최단거리였던 w(p), 즉 기존 w( p𝑥𝑦 )를 가진 경로보다 w( p'𝑥𝑦 )를 가진 w(p')가 더 작기 때문에

w(p') < w(p)이 되므로, 이는 모순이 발생하게 됩니다.

사이클 Cycle

최단 경로는 사이클을 포함할 수 없습니다. 왜냐면 위에서 얘기했던 음수 가중치 사이클을 가질 수 없기 때문입니다.

양수 가중치 사이클이 존재할 경우, 해당 사이클을 생략함으로써 더 짧은 경로를 얻을 수 있습니다. 

즉, 사이클을 포함하는 경로는 최단 경로가 아닙니다.

제로 가중치 사이클이 있을 경우, 이를 사용할 이유가 없습니다. 

따라서 최단 경로를 찾는 과정에서 이러한 사이클은 고려하지 않는다고 가정합니다.

Single-Source 최단 경로의 Output

Vertex V의 모든 원소 v에 대해서 얘기합니다. 즉 v ∈ V

d[v]=δ(s, v) : 정점 s에서 정점 v까지의 최단 경로 가중치입니다.

초기값으로 d[v] = ∞로 설정됩니다.

알고리즘이 진행됨에 따라 이 값은 줄어들 수 있지만, 항상 d[v] ≥ δ(s, v)를 유지해야 합니다.

즉, 항상 최단 경로보다 같거나 큰 값이어야한다는겁니다.

d[v]는 "최단 경로 추정치(shortest-path estimate)"라고 불립니다.

π[v] : 정점 v에 대한 최단 경로에서의 전임자(predecessor)입니다.

만약 전임자가 없다면, π[v]=NIL로 설정됩니다.

π 배열은 최단 경로 트리를 형성합니다. 즉, 최단 경로를 나타내는 트리 구조입니다.

초기화

모든 최단 경로 알고리즘은 이 초기화 단계로 시작합니다. 이 단계에서는 그래프의 모든 정점에 대해 초기 값을 설정합니다.

의사 코드를 보시겠습니다.

각 정점 v에 대해 :

d[v]를 무한대(∞)로 설정합니다. 

이는 초기 상태에서 모든 정점까지의 최단 경로 가중치가 알려지지 않음을 의미합니다.
π[v]를 NIL로 설정합니다. 이는 해당 정점에 대한 전임자가 없음을 나타냅니다.

출발 정점 s에 대해서는 d[s]를 0으로 설정합니다. 이는 출발점에서 자기 자신까지의 거리는 0임을 의미합니다.

아래 코드에 주석을 달아봤습니다.

INIT-SINGLE-SOURCE(V, s)
    // V: 그래프의 모든 정점 집합
    // s: 출발 정점

    for each v ∈ V // 그래프의 모든 정점 v에 대해 반복
        do d[v] ← ∞ // 정점 v까지의 최단 경로 가중치를 무한대로 초기화
            π[v] ← NIL // 정점 v의 전임자를 NIL로 초기화 (전임자가 없음)

    d[s] ← 0 // 출발 정점 s에서 자기 자신까지의 거리는 0으로 설정

★ 간선 완화 Relax

간선 (u,v)를 완화하는 과정입니다. 

이는 정점 u에서 정점 v로 가는 경로를 통해 v까지의 최단 경로 가중치를 계속 업데이트하는 과정입니다.

의사 코드를 보시겠습니다.

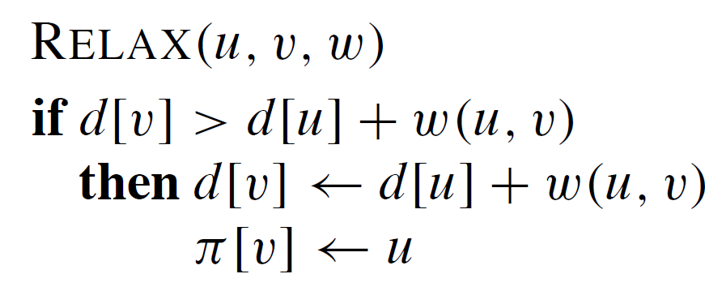
의사 코드에 주석 달아봤습니다.

RELAX(u, v, w)
    // u: 시작 정점
    // v: 도착 정점
    // w: 간선 (u, v)의 가중치

    if d[v] > d[u] + w(u, v) then
        // 만약 v까지의 현재 최단 경로 가중치가
        // u에서 v로 가는 경로를 통해 얻은 가중치보다 크면
        d[v] ← d[u] + w(u, v) // v까지의 최단 경로 가중치를 업데이트

        π[v] ← u // v의 전임자를 u로 설정하여 최단 경로를 추적할 수 있도록 함

조건: d[v]가 d[u] + w(u, v)보다 크면 d[v]를 d[u] + w(u, v)로 업데이트합니다.

이는 u를 거쳐 v로 가는 경로가 더 짧다는 것을 의미합니다.

π[v]를 u로 설정하여 v의 전임자를 u로 업데이트합니다.

예시로 

그래프에서 간선 (u, v)의 가중치가 10일 때, u에서 v로 가는 경로를 완화하는 과정을 보여줍니다.

d[v] = 10, source 정점에서 u정점까지 weight가 4, u에서 v로 가는 간선의 weight가 3인 상황입니다.

d[u]+w(u, v)가 더 작으면 d[v]를 업데이트합니다.

그래서 u에서 v로 갈 때 4 + 3이니 더 작아서 10 -> 7로 업데이트합니다.

이제 d[v] = 7이 되었네요.

하나 더 보시면 u에서 v로 갈 때 4 + 3으로 7 weight를 가지지만

기존 경로 d[v] = 6이므로 더 작습니다.

그럼 업데이트할 필요가 없으니 그대로

d[v] = 6인거죠

부록

정리해보면 Single-source 최단 경로 찾기 문제는 INIT-SINGLE-SOURCE로 초기화한 뒤에 relax edges 과정을 거칩니다.

알고리즘에 따라 순서와 각 간선을 완화하는 횟수가 다릅니다.

이전 시간까지 Minimal Spanning Tree, 즉 MST를 구하는 기본적인 방법을 배워봤습니다.
이번엔 MST를 구하는 두 가지 방법 중 두 번째 프림 알고리즘을 배워볼겁니다. 

- Kruskal’s Algorithm 
- Prim’s Algorithm (오늘 배울거)

참고 : 가벼운 간선과 같은 용어를 모르신다면 MST를 공부하시면 됩니다.

https://kimyir.tistory.com/133

프림 알고리즘은 항상 하나의 트리를 구축합니다. 

즉, 알고리즘이 진행되는 동안 항상 연결된 트리 구조를 유지합니다.

프림 알고리즘의 시작은 임의의 정점(루트)에서 시작합니다. 이 정점은 MST의 시작점이 됩니다.

이걸 r이라고 하겠습니다.

각 단계에서 MST에 포함된 정점 집합 V𝐴 와 포함되지 않은 정점 집합 V − V𝐴 사이의 "가벼운 간선(light edge)"을 찾습니다.
가벼운 간선은 MST에 추가할 수 있는 최소 가중치의 간선입니다.

선택된 가벼운 간선을 MST에 추가하고, 해당 간선에 연결된 정점을 MST에 포함시킵니다.

정리하자면 

1. 현재 MST에 포함된 정점 집합 V𝐴 를 유지합니다.

2. V𝐴 와 V − V𝐴 사이의 가벼운 간선을 찾습니다.
3. 이 간선을 MST에 추가하고, 해당 간선에 연결된 정점을 V𝐴에 포함시킵니다.
4. 모든 정점이 MST에 포함될 때까지 이 과정을 반복합니다.

의사코드

프림 알고리즘에서는 우선순위 큐(Q)를 사용하여 가벼운 간선을 효율적으로 찾습니다.
큐의 각 객체는 MST에 포함되지 않은 정점  V − V𝐴 에 들어있습니다.

각 정점 v의 키 값은 MST에 포함된 정점 u와의 간선 중 최소 가중치를 나타냅니다. 

즉, u ∈ V𝐴 인 모든 간선 (u, v)의 최소 가중치입니다.
이 키 값은 해당 정점이 MST에 추가될 때의 가중치를 나타냅니다.

우선순위 큐에서 EXTRACT-MIN 연산을 수행하면, MST에 추가할 정점 v가 반환됩니다.
이 정점은 MST에 포함된 정점 V𝐴와 연결된 가벼운 간선을 가진 정점입니다.

만약 정점 v가 MST에 포함된 정점과 인접하지 않다면, 그 키 값은 무한대(∞)로 설정됩니다. 

이는 해당 정점이 현재 MST에 추가될 수 없음을 나타냅니다.

다시 정리하자면

알고리즘의 입력으로 주어진 루트 정점 r에서 시작합니다. 이 정점은 MST의 시작점이 됩니다.
r는 알고리즘에 입력으로 주어지지만, 임의의 정점이 될 수 있습니다.

각 정점은 트리에서 자신의 부모를 알고 있습니다. 이 정보는 π[v]라는 속성으로 저장됩니다.

π[v]는 정점 v의 부모를 나타내며, 루트 정점 r의 경우 π[v]=NIL로 설정됩니다. 

이는 루트 정점이 부모가 없음을 의미합니다.

해당 공식은 알고리즘 진행되면서 MST에 포함되지 않은 정점 집합 V−{r}−Q에 대해 각 정점과 그 부모 정보를 저장합니다.

알고리즘이 종료되면, V𝐴 = V가 되고 Q = ∅이 됩니다. 큐가 비게 됩니다. 즉, 모든 정점이 MST에 포함됩니다.

결국 MST는 이렇게 표현됩니다.

시간 복잡도

시간 복잡도는 우선순위 큐가 어떻게 구현되었는지에 따라 달라집니다. 이진 힙(binary heap)을 사용한다고 가정합시다.

우선순위 큐 Q를 초기화하고 첫 번째 for 루프를 수행하는 데 필요한 시간 복잡도는 O(V log V)입니다.
여기서  V는 정점의 수입니다.

루트 정점 r의 키 값을 감소시키는 데 필요한 시간 복잡도는 O(log V)입니다.

  
|V|번의 EXTRACT-MIN 호출이 필요하므로, 이 부분의 시간 복잡도는 O(V log V)입니다.

간선의 수 |E|에 비례하여 DECREASE-KEY 호출이 발생하므로, 이 부분의 시간 복잡도는 O(E log V)입니다.

결국 다 더하면 O(V log V)+O(E log V)가 되지만, 일반적으로 |E|가 |V|² O(E logV)가 더 지배적인 항이 됩니다.

이 내용은 전포스팅 크루스칼 알고리즘에서도 다뤘습니다. 따라서 O(V log V)는 생략해도 됩니다.

결론적으로 프림알고리즘의 시간복잡도는 O(E log V) 입니다.

크루스칼 알고리즘 vs 프림 알고리즘

크루스칼 알고리즘:

간선 중심의 접근 방식입니다. 

모든 간선을 가중치에 따라 정렬한 후, 가장 낮은 가중치의 간선부터 선택하여 MST에 추가합니다.
사이클을 형성하지 않도록 유니온-파인드 자료구조를 사용하여 간선을 선택합니다.

프림 알고리즘:

정점 중심의 접근 방식입니다. 

임의의 정점에서 시작하여 MST에 포함된 정점과 포함되지 않은 정점 사이의 가벼운 간선을 선택하여 MST를 확장합니다.
현재 MST에 연결된 정점과 연결되지 않은 정점 사이의 최소 가중치 간선을 선택합니다.

부록

만약 경로의 weight, 가중치가 마이너스라면 알고리즘이 작동할까요?

네 그래도 알고리즘이 작동됩니다.

이전 시간까지 Minimal Spanning Tree, 즉 MST를 구하는 기본적인 방법을 배워봤습니다.

이제부턴 Minimal Spanning Tree를 구하는 두 가지 방법 중 첫 번째 크루스칼 알고리즘을 배워볼겁니다. 

- Kruskal’s Algorithm (오늘 배울거)

- Prim’s Algorithm

정의

크루스칼 알고리즘은 결국 MST처럼 최소 비용의 경로를 찾는겁니다. 그전에 정의부터 설정하겠습니다.

그래프 G는 비방향 가중치 그래프입니다.

w : E→R

w는 가중치고 E는 그래프 G의 간선 집합입니다. R은 실수 집합입니다.

즉, w는 간선 집합 E의 각 간선에 대해 실수 값을 매핑하는 가중치 함수입니다. 

알고리즘은 각 정점이 자신의 컴포넌트로 시작합니다. 즉, 초기에는 모든 정점이 독립적으로 존재합니다.

알고리즘은 반복문을 돌려서 두 개의 컴포넌트를 선택하여 연결하는 Light edge를 선택하여 병합합니다. 

이 간선은 컷을 가로지르는 가장 작은 가중치의 간선입니다.

뜻이 뭔지 모르겠다면 저번 포스팅을 다시 보시면 됩니다.

https://kimyir.tistory.com/133

간선 집합을 가중치에 따라 오름차순으로 스캔합니다. 즉, 가장 작은 가중치의 간선부터 선택합니다.

알고리즘은 불일치 집합(Disjoint Set) 자료구조를 사용하여 간선이 서로 다른 컴포넌트를 연결하는지 확인합니다. 

이를 통해 사이클을 방지합니다.

그럼 이를 통해 의사코드를 보시겠습니다.

의사코드

코드를 분석해봅시다.

A를 초기화 : O(1) -> MST 집합 A를 초기화하는 데 상수 시간이 소요됩니다.

첫 for 반복문 : |V| MAKE-SETs -> 각 정점에 대해 MAKE-SET을 호출하므로 O(|V|)의 시간이 소요됩니다.

E를 정렬 : O(E logE)  -> 간선 집합 E를 가중치에 따라 정렬하는 데 걸리는 시간입니다.
두 번째 for 반복문 : O(E) FIND-SETs and UNIONs -> 각 간선에 대해 FIND-SET과 UNION을 호출하므로 O(E)의 시간이 소요됩니다.

Find - SET과 Unions에 대해서 아래에서 설명드리겠습니다.

불일치 집합 데이터 구조

disjoint-set data structure, 즉 불일치 집합 자료구조를 사용하여 효율적으로 FIND-SET과 UNION을 수행합니다.

불일치 집합 자료구조(Disjoint Set Data Structure), 또는 유니온-파인드(Union-Find) 자료구조는 서로 겹치지 않는 집합을 효율적으로 관리하기 위한 자료구조입니다. 

Find : 특정 원소가 속한 집합의 대표 원소(루트)를 찾는 연산입니다. 이 연산은 경로 압축(Path Compression)을 통해 최적화할 수 있습니다.
Union : 두 개의 집합을 하나로 합치는 연산입니다. 이 연산은 union by rank 또는 union by size 기법을 사용하여 트리의 높이를 최소화합니다.

예시 

1. 의사 코드에 있던 과정처럼 초기화를 먼저합니다.

각 Vertex 별로 하나의 Component를 생성합니다. Disjoint-set |V|개를 생성합니다.
초기화하면 {a}, {b}, {c}, {d}, {e}, {f}, {g}, {h}, {i} 로 구성된 Set이 만들어집니다.

2. 간선의 가중치 오름차순으로 정렬합니다.

weight가 가장 작은 1부터 12까지 정렬합니다.

3. 간선 선택 후 Union 연산합니다.

가장 작은 가중치 1이었던 간선(c, f)를 먼저 선택합니다.

find(c)와 find(f)를 통해 두 정점이 연결되어 있지 않음을 확인합니다.
union(c, f)를 수행하여 집합을 합칩니다.
결과 집합: {a}, {b}, {c, f}, {d}, {e}, {g}, {h}, {i}

그 다음으로 작은 가중치인 2 간선(g, i)를 선택합니다.

find(g)와 find(i)를 통해 두 정점이 연결되어 있지 않음을 확인합니다.
union(g, i)를 수행하여 집합을 합칩니다.
결과 집합: {a}, {b}, {c, f}, {d}, {e}, {g, i}, {h}

그 다음으로 작은 가중치인 3 간선 (e, f)를 선택합니다.

find(e)와 find(f)를 통해 두 정점이 연결되어 있지 않음을 확인합니다.
union(e, f)를 수행하여 집합을 합칩니다.
결과 집합: {a}, {b}, {c, e, f}, {d}, {g, i}, {h}

이런 식으로 계속 진행하여 모든 정점이 연결될 때까지 반복합니다. 

각 단계에서 사이클이 형성되지 않도록 주의하며, 최종적으로 최소 신장 트리를 구성하게 됩니다.

크루스칼 알고리즘으로 결과적으로 생성된 MST 결과입니다.

시간 복잡도

크루스칼 알고리즘의 첫 번째 단계는 모든 간선을 가중치에 따라 정렬하는 것입니다.
이 단계의 시간 복잡도는 O(E log E)입니다. 

여기서 E는 간선의 수입니다. 정렬 알고리즘의 일반적인 시간 복잡도가 로그 시간 복잡도를 포함하기 때문입니다.

두 번째 단계는 각 간선을 선택할 때마다 find와 union 연산을 수행하는 것입니다.
이 연산의 시간 복잡도는 O(E α(V))입니다. 여기서 α는 아커만 함수의 역함수로, 매우 느리게 증가하는 함수입니다. 

사실상 이 값은 거의 상수에 가깝습니다.

이제 이 연산을 간선 뿐 아니라 정점에도 사용하면 정점 갯수만큼 더해준 값에 아커만 곱해주면 되겠죠?

따라서 정리해보면

O( (V + E) α(|V|) ) + O(E log E) 이 나오게 됩니다.

|E| ≤ |V|² : 간선의 수는 정점의 수의 제곱 이하입니다.

즉, 완전 그래프의 경우 모든 정점이 서로 연결되므로 최대 간선 수는 |V|²입니다.

|E|가 |V|² 이하이므로, 양변에 로그를 취하면 lg |E| ≤ lg (|V|²) = 2 lg |V|가 됩니다.

 lg |E|는 O(lg |V|)와 같고, 이는 O(lg E)로 표현할 수 있습니다.

|E| ≥ |V| − 1 : 간선을 다 연결하면 노드에서 1 빼주면 간선의 수가 나옵니다.

연결 그래프에서 |E|가 |V| - 1 이상이므로, 전체 시간 복잡도는 O(E α(V)) + O(E log E)로 표현됩니다.

O(Eα(|V|)) + O(E logE) 에서 아커만 함수는 거의 상우에 가깝기 때문에 생략해도 됩니다.
따라서, O(E log E): 전체 시간 복잡도는 간선의 수에 따라 로그 시간 복잡도를 가집니다.

하지만 위에서 말했듯이 log |E|는 O log|V|와 같다고 했죠?

그래서 O(E log V) 로 표현해도 맞긴합니다.

어쨋든 크루스칼 알고리즘의 실행 시간 시간 복잡도는 간선의 수에 따라

O ( E log E) 입니다.

최소 신장 트리(MST)를 이해하면 두 가지 주요 알고리즘인 크루스칼 알고리즘과 프림 알고리즘을 효과적으로 적용할 수 있습니다. 

문제 정의

한 마을에는 집과 도로가 있습니다.
각 도로는 두개의 집만 연결합니다.
두 집 House u와 House v를 연결하는 도로의 수리 비용은 w(u,v)입니다. 

목표

모든 집이 서로 연결되도록 충분한 도로를 수리하되, 수리 비용이 최소가 되도록 해야 합니다.
즉, 모든 집이 서로 도달 가능해야 하며, 총 수리 비용이 최소화되어야 합니다.

그래프 정의

• 비방향 그래프 G=(V,E)로 구성되어 있습니다.
• V: 정점(집)
• E: 간선(도로)

각 간선 (u,v)에 대해 가중치 w(u,v)가 정의되어 있습니다. 

이는 도로의 수리 비용을 나타냅니다.

목표

T⊆E 를 찾아야 합니다.
1. T는 모든 정점을 연결해야 하며, T는 신장 트리(spanning tree)입니다.
2.

이 식이 최소화되어야 합니다. 

즉, 선택된 간선(u, v)쌍의 총 가중치(비용)가 최소가 되어야 합니다.

정리하자면 모든 신장 트리 중에서 가중치가 최소인 신장 트리를 최소 신장 트리(MST)라고 합니다.

예시

사진에 보시다시피 회색으로 칠해진 간선들은 모든 정점을 연결하면서도 총 가중치가 최소인 간선들입니다.

이 간선들이 바로 Minimum Spanning Tree, 즉 MST입니다.

하나의 그래프에 여러 개의 MST가 존재할 수 있습니다.

예를 들어, MST 간선 (e,f)를 그냥 간선 (c,e)로 교체하면, 새로운 다른 신장 트리 MST`가 생성되지만 가중치는 동일합니다.

MST의 속성

간선 수: MST는 | V | − 1개의 간선을 가집니다. (여기서 |V|는 정점의 수), 트리이기 때문에 간단히 생각하면됩니다.

즉, 모든 정점을 연결하면서도 최소한의 간선만 사용합니다. 

사이클 없음: MST는 사이클을 포함하지 않습니다. No Cycle.

비방향이기 때문에 사이클이 존재할 수가 없습니다.

유일하지 않을 수 있음: MST는 여러 개 존재할 수 있습니다. 다른 MST`가 존재가능한거죠.

MST 구하는 법

1. 간선의 집합 A를 구축합니다. 처음에는 A에 간선이 없습니다.

2. 루프 불변 조건: 반복문으로 간선을 A에 추가할 때마다 "A는 어떤 MST의 부분 집합이다"라는 조건을 유지해야 합니다.

즉, 추가하는 간선이 MST의 일부가 될 수 있어야 합니다. 루프 불변이니 반복문의 참인 조건이죠.
3. 간선 (u,v)가 A에 추가될 때, A가 어떤 MST의 부분 집합이여야합니다. 이를 위해 안전한 간선만 추가합니다. 

즉, 이 과정을 정리한 식은 A∪{(u,v)}인데, 이 집합 A가 어떤 MST의 부분 집합이 되어야 한단겁니다.

MST 구하는 의사 코드

입력: 인자로 각각 그래프 G와 각 간선의 가중치 w를 받습니다.
출력: 최소 신장 트리 A

과정을 보자면

초기화: A를 빈 집합으로 설정합니다.
반복문: A가 신장 트리가 아닐 때까지 반복합니다. 안전한 간선(u, v)을 찾아서 A에 추가합니다.
결과 반환: 최종적으로 A를 반환합니다.

몇가지 개념 정의

S ⊂ V, A ⊆ E라고 가정하도록합시다.

Cut : 그래프의 집합 V를 S 집합과 V−S 집합으로 정점을 나누는 파티션입니다.

사진에서는 그냥 반으로 S 집합과 V - S 집합으로 나눴습니다.

Cross : 간선 (u,v)가 컷 (S, V−S)를 교차한다고 할 때,

u의 한 끝점이 S에 있고, 다른 끝점 v가 V−S에 있을 때 그 간선이 크로스하고 있다고 합니다.

사진에서는 파란선들이 Cut에 덮여있으니 이 간선들이 Cross입니다.

Respects : 컷이 집합 A를 존중한다고 할 때, A의 어떤 간선도 컷을 교차하지 않는 경우를 의미합니다.

다시 말하자면 안전한 간선이란 MST에 포함가능한 간선입니다.

즉, 모든 간선 중에서 가중치가 가장 낮은 간선입니다.

그리고 집합 A에 들어가는 간선들은 모두 안전한 간선들만 들어갑니다.

이 때 집합 A의 간선들이 Cross 하는 간선들이 아니라면 컷이 집합 A를 존중한다고 하는겁니다.

이게 왜 필요하냐면 컷을 나누는 과정에서 집합 A의 간선이 포함되지 않도록 하는 조건을 위해섭니다. 

Light Edge : 컷을 교차하는 간선 중에서 가중치가 최소인 간선을 의미합니다. 

즉, 주어진 컷을 교차하는 모든 간선 중에서 가장 가벼운 간선입니다. 하나의 컷에 여러 Light Edge가 존재 가능합니다.

Respects와 다르게 컷을 교차하는, 즉 컷을 지나는 간선만 해당됩니다. 그중에서 가중치가 가장 낮은 간선이죠.

위 이미지에서의 세 파란 Cross 간선 중 왼쪽부터 3 6 1이라면 가장 오른쪽의 파란 cross 간선이 Light Edge,

이미지처럼 1 6 1이라면 두 1 간선들이 모두 Light Edge입니다.

이 Light Edge는 굉장히 중요합니다. 반복적으로 Light Edge만 찾다보면 MST가 완성되기 때문입니다.

아래 중심 정리에서 설명드리겠습니다.

중심정리 Central Theorem

1. 집합 A가 어떤 MST의 부분 집합이라고 가정합니다.
2. (S, V−S)는 집합 A를 존중하는 컷입니다.
3. (u, v)는 컷 (S, V−S)를 가로지르는 라이트 엣지입니다.
4. 그러면 (u, v)는 집합 A에 대해 안전한 간선입니다.

증명 과정

이 중심정리를 한번 정리해봅시다. (u,v)가 안전한 간선이라는 것을 보여주는 것이 목표입니다.

T를 집합 A를 포함하는 MST라고 가정합니다.
(a) 만약 T가 (u,v)를 포함한다면, 증명이 완료됩니다.

(u, v)가 안전한 간선이니까 MST에 포함되는겁니다.
(b) 만약 T가 (u,v)를 포함하지 않는다면, 이제 좀 어려워집니다.

방식은 A와 {(u,v)}를 포함하는 다른 MST′ 를 구성하는겁니다.

일단 b의 상황을 봅시다.

트리에서는 각 정점 쌍 사이에 유일한 경로가 존재합니다. 즉, 두 정점 u와 v 사이에는 오직 하나의 경로만 있습니다.

지금 사진엔 u와 v 사이가 실선으로 되어있는데 아직은 u와 v가 연결안되어있어요. 간선 (u, v)는 연결안되어있습니다.

T가 MST이므로, u와 v 사이에 유일한 경로 p가 존재합니다. 

이 경로는 컷 (S, V−S)를 최소한 한 번은 가로질러야 합니다.

경로라는게 중요합니다. 여러 간선들이 구성되는 경로입니다.

경로 p의 엣지 중 하나를 (x, y)라고 할 때, 이 엣지는 컷을 가로지릅니다. 사진에서는 회색선에 진한 검은색 선 보이시죠?

(u, v)를 선택할 때, 이 엣지의 가중치는 w(u, v)로 표현됩니다. 그리고 (x, y)의 가중치는 w(x, y)로 표현됩니다.
따라서, w(u, v) ≤ w(x, y)가 성립해야 합니다. 이는 (u, v)가 라이트 엣지라는 정의와 일치합니다.

웬 대소비교가 나오냐면 우리가 지금 MST를 찾아내야하기 때문에 u와 v의 간선은 무조건 가중치가 젤 낮겠죠?

만약 w(u, v)가 더 크다면 굳이 이걸 고를 필요없이 (x, y)을 골랐겠죠.

컷이 집합 A를 존중하므로, 엣지 (x, y)는 집합 A에 포함되지 않습니다.

즉, (x, y)는 컷을 가로지르지만, 집합 A에는 속하지 않는 간선입니다.

이번엔 아까 말했던 새로운 트리 T' 를 만들어봅시다.

우선 기존 MST T에서 (x, y)를 제거하여 두 개의 컴포넌트로 나눕니다.

그런 다음, 간선 (u, v)를 추가하여 두 컴포넌트를 다시 연결합니다.

이 때 기존 MST w(T) ≥ MST w(T)' 가 만족됩니다.

왜냐면 w(u, v) ≤ w(x, y)가 성립되기 때문에 우린 u, v를 라이트 엣지로 설정했으니까

당연히 기존 (x, y) 간선을 연결한 w(T)가 더 크거나 같은거죠. 증명 끝.

이제 이 공식을 봅시다.

새로운 MST T'는 기존 T 에서 (x, y) 간선을 빼기, 즉 제거한 뒤 (u, v)를 합집합, 즉 (u, v)를 추가한겁니다.

결국 T′ 는 스패닝 트리입니다. 모든 정점을 포함하고 연결되어 있기 때문입니다.

가중치 공식도 봅시다.

새로운 MST T'는 기존 T의 가중치 - 간선(x, y)을 제거했으니 가중치를 빼줍니다.

그리고 새로운 간선 w(u, v)를 추가했으니 가중치를 더해줍니다.

이 가중치의 결과물이 바로 MST T'의 가중치입니다.

w(T') ≤ w(T)는 위에 증명에서 말했듯이 라이트 엣지 때문에 무조건 라이트 엣지 (u, v)를 가진 T' 가 더 작거나 같습니다.

마지막으로 (u, v)가 집합 A에 대해 안전한 간선임을 보여야 합니다.

집합 A가 기존 MST T에 포함되고, 간선 (x, y)가 A에 포함되지 않으므로, A는 새로운 MST T′에도 포함됩니다.

그리고 A와 (u, v)를 합친 집합이 새로운 MST T′ 에 포함됩니다.

새로운 MST T′ 가 MST이므로, (u, v)는 안전한 간선으로 인정받습니다.

즉, (u, v)가 MST에 포함될 수 있음을 의미합니다.

부록

C는 그래프 G 𝐴 의 연결된 컴포넌트를 나타냅니다. 

여기서 G 𝐴 는 정점 집합 V와 간선 집합 A로 구성된 그래프입니다.

만약 (u, v)가 컴포넌트 C와 G 𝐴 의 다른 컴포넌트와 연결되는 라이트 엣지라면, 컷 (V𝐶, V − V𝐶)를 가로지르는 간선일겁니다. 

이 때 (u, v)는 집합 A에 대해 안전하다는 것입니다.

즉, 이 간선은 MST에 포함될 수 있습니다.

갑자기 든 생각이지만 만약 Minimum Spanning Tree가 아닌 Maximum Spanning Tree를 구하려고 하면 어떻게 될까요?

Light Edge : 컷을 교차하는 간선 중에서 가중치가 최소인 간선을 의미합니다. 

이 정의를 거꾸로 해서 최소가 아닌 최대인 간선을 찾는것으로 바꾸면 다 반대가 되기 때문에 구할 수 있겠죠?

어쨋든 오늘 알아본 MST의 아이디어로 뒤에 설명할 Kruskal Algorithm에 사용됩니다. 다음 포스팅에 다시 다뤄봅시다.